7.3. Measures
The Riemann integral is certainly useful (and complicated) enough, but it does have a few limitations and oddities:| Examples 7.3.1:Oddities of Riemann Integral | |
| |
We therefore want to define another concept of integration that is more general than the Riemann integral, yet retains the "good" properties of that integral.
One of the limitations of the Riemann integral is that it is based on the concept of an "interval", or rather on the length of subintervals [xj-1, xj]. We therefore need to find a generalization of the "length" concept of a set in the real line. That new "length" concept, which we will call "measure", should satisfy two key conditions:
To define what will eventually be called Lebesgue Measure, we follow a two-stage strategy:
- The new "measure" concept should be applicable to intervals, unions of intervals, and to more general sets (such as a Cantor set). Ideally, it should be defined for all sets.
- The new "measure" concept should share as many properties as possible with the standard length of an interval, such as:
- the 'measure' of a set should be non-negative
- the 'measure' of an interval should be the length of that interval
- the 'measure' of countably many disjoint sets should be the sum of the 'measures' of the individual sets
- Stage One:
- We will define a concept extending length that is defined for all sets (to satisfy condition 1 above)
- Stage Two:
- We will modify that concept so that it looks as close as possible to the standard length concept (to satisfy condition 2 above)
| Definition 7.3.2: Outer Measure | |
If A is any subset of R, define the (Lebesgue) outer
measure of A as:
m*(A) = inf {where the infimum is taken over all countable collections of open intervals An such that A 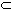
 An
and l(An) is the standard length of the
interval An. An
and l(An) is the standard length of the
interval An.
| |
Note that it is possible to define other outer measures without using the concept of length of intervals, so the above outer measures is but one of many. In fact, this particular outer measure is called the Lebesque outer measure, but we will not talk about any other outer measure in this chapter, so whenever we say "outer measure" we really mean "Lebesque outer measure".
| Examples 7.3.3: Outer Measure of Intervals | |
| |
| Proposition 7.3.4: Properties of Outer Measure | |
Outer measure has the following properties:
| |
Since outer measure is defined for all sets in R, our first key
condition above is satisfied. But outer measure is not quite similar to a
length, because it is only subadditive (
m*(A 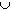 B)
B)
 m*(A) +
m*(B)
), not additive (
m*(A
m*(A) +
m*(B)
), not additive (
m*(A 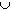 B)
=
m*(A) +
m*(B)
for disjoint sets A and B). Therefore one of the
requirements of the second key condition is not satisfied.
B)
=
m*(A) +
m*(B)
for disjoint sets A and B). Therefore one of the
requirements of the second key condition is not satisfied.
| Examples 7.3.5: Properties of Outer Measure | |
| |
To make our outer measure additive, something has to give. We decide to restrict the domain to gain countable additivity, which will result in our stage-two definition.
Actually, there are several ways to restrict an outer measure. A somewhat intuitive way,
perhaps, is to define an inner measure m* that is
similar to the outer measure but involves a sup over suitable sets.
Then sets for which
m*(A) = m*(A) are called
measurable and the restriction of the outer (or inner) measure to the
measurable sets is called a measure. Another idea is to define a set
E as measurable if it is "almost" an open set, in the sense that for every
 > 0
there exists an open set
U
> 0
there exists an open set
U 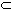 R
such that
m*(U \ E)
R
such that
m*(U \ E) 
 .
This is an idea known as one of Littlewood's three principles, which is
helpful enough, but we will choose yet another approach due to Caratheodory that
is (hopefully) less abstract and (somewhat) easier to work with.
.
This is an idea known as one of Littlewood's three principles, which is
helpful enough, but we will choose yet another approach due to Caratheodory that
is (hopefully) less abstract and (somewhat) easier to work with.
| Definition 7.3.6: Measurable Sets and Lebesgue Measure | |
A set E is (Lebesque) measurable if for every set A
we have that
m*(A) = m*(AIf E is measurable, the non-negative number m(E) = m*(E) is the (Lebesgue) measure of the set E. | |
m*(A) = m*( (ATherefore, to show that a set E is measurable it is sufficient to prove thatE)
(A
comp(E)) )
m*(A
E) + m*(A
comp(E))
m*(A)The motivation for this definition is that it ensures that for two disjoint measurable sets E and F we have thatm*(A
E) + m*(A
comp(E))
m(Eas we will show later, i.e. measure is additive.F) = m(E) + m(F)
| Examples 7.3.7: Measurable Sets | |
| |
The next result shows that a measure has all of the properties of a length: the measure of an interval is its length, and the measure of countably many disjoint sets it is additive. But, as we mentioned before, the price we have to pay for that is that it is no longer defined for all sets.
| Theorem 7.3.8: Properties of Lebesgue measure | |
| |
Sometimes we refer to the collection of all open sets, closed sets, and sets that can be derived from them as Borel sets. Its significance for our discussion is that all Borel sets are measurable. So, instead of listing open sets, closed sets, unions of them, intersections of them, etc. we refer to them collectively as Borel sets. However, it is important to note that not every Borel set is a union or intersection of open/closed sets, and unions/intersections of those, etc., so that the Borel sets are really something new. But these details would lead us to far afield.
| Theorem 7.3.9: Borel sets are measurable | |
| The collection of Borel sets is the smallest sigma-algebra which contains all of the open sets. Every Borel set, in particular every open and closed set, is measurable. | |
After all this theory it is time to consider some easier examples, including the measure of some well-known sets that are not intervals (whose measure, as we know by now, are their length).
Outer measure is defined for all sets, and according to the above list of properties, most "common" sets such as intervals, closed or open sets, unions and intersections of measurable sets are all measurable. But we have to pay for the property that measure is (countably) additive with the fact that not every set is measurable, as we will see shortly. First, let's take a quick look into sets that arise in conjunction with functions? First, let's establish some equivalency conditions.
| Proposition 7.3.11: Equivalent Measurable Sets | |
Let f be a real-valued function with a measurable set as domain.
Then the following are quivalent:
| |
Note that this does not say that each or any of these sets are indeed measurable. It does say that if any of these four sets are measurable, then the remaining ones are also measurable. An easy case in which one of these sets is clearly measurable is described next.
| Proposition 7.3.12: Inverse Images are Measurable | |
| If f is a continuous function with a measurable set as domain, then the sets f -1(a, b), f -1(a, b], f -1[a, b), and f -1[a, b] are all measurable for any (extended) real numbers a < b. | |
So here we have further examples of sets that are measurable. But not all is roses, and you can't always have your cake and eat it, too: we do have to pay for the property that measure is (countably) additive with the fact that not every set is measurable.
| Proposition 7.3.13: Not all Sets are Measurable | |
| There are sets that are not (Lebesgue) measurable, i.e. not every set is (Lebesgue) measurable. | |
It is therefore true that not every set is measurable, but it is fair to say that most sets are.
To summarize, we introduced a new concept called measure in two stages, each of which had a typical "good news, bad news" property.
- In the first stage we defined outer measure.
- good news: outer measure is defined for all sets.
- bad news: outer measure is not additive, i.e. it is not quite comparable to a length.
- In the second stage we defined measure by restricting outer
measure to the measurable sets.
- good news: measure is additive, i.e. it is a good generalization of length.
- bad news: measure is not defined for all sets
| Proposition 7.3.14: Monotone Sequences of Measurable Sets | |
If { An } is a sequence of measurable sets
that is decreasing, i.e.
Aj 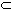 Aj+1
for all j, and m(A1) is
finite, then Aj+1
for all j, and m(A1) is
finite, then
lim m(Aj) = m(If { An } is a sequence of measurable sets that is increasing in the sense that Aj+1 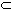 Aj
for all j, then Aj
for all j, then
lim m(Aj) = m( | |
| Examples 7.3.15: Monotone sequences of measurable sets | |
| |
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 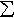 l(An) }
l(An) }
 )
is measurable.
)
is measurable.