7.4. Lebesgue Integral
We previously defined the Riemann integral roughly as follows:
- subdivide the domain of the function (usually a closed, bounded interval) into finitely many subintervals (the partition)
- construct a simple function that has a constant value on each of the subintervals of the partition (the Upper and Lower sums)
- take the limit of these simple functions as you add more and more points to the partition.
If the limit exists it is called the Riemann integral and the function is called Riemann integrable. Now we will take, in a manner of speaking, the "opposite" approach:
- subdivide the range of the function into finitely many pieces
- construct a simple function by taking a function whose values are those finitely many numbers
- take the limit of these simple functions as you add more and more points in the range of the original function
If the limit exists it is called the Lebesgue integral and the function is called Lebesgue integrable. To define this new concept we use several steps:
- we define the Lebesgue Integral for "simple functions"
- we define the Lebesgue integral for bounded functions over sets of finite measure
- we extend the Lebesgue integral to positive functions (that are not necessarily bounded)
- we define the general Lebesgue integral
First, we need to clarify what we mean by "simple function".
| Definition 7.4.1: Characteristic and Simple Function | |
For any set A the function
is called the characteristic function of A. A finite linear combination of characteristic functions s(x) =is called simple function if all sets Ei are measurable. | |
A function f defined on a measurable set A that takes no more than finitely many distinct values a1, a2, ... , an can always be written as a simple function
f(x) =an XAn(x)
where
An = { xA: f(x) = an }
Therefore simple functions can be thought of as dividing the range of f, where the resulting sets An may or may not be intervals.
| Examples 7.4.2: Simple Functions | |
| |
For simple functions we define the Lebesgue integral as follows:
| Definition 7.4.3: Lebesgue Integral for Simple Function | |
If
s(x) = 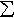 an
XAn(x)
is a simple function and m(An) is finite
for all n, then the Lebesgue Integral of s
is defined as
an
XAn(x)
is a simple function and m(An) is finite
for all n, then the Lebesgue Integral of s
is defined as
If E is a measurable set, we define
| |
| Example 7.4.4: Lebesgue Integral for Simple Functions | |
| |
Just as step functions were used to define the Riemann integral of a bounded function f over an interval [a, b], simple functions are used to define the Lebesgue integral of f over a set of finite measure.
| Definition 7.4.5: Lebesgue Integral for Bounded Function | |
Suppose f is a bounded function defined on a measurable set
E with finite measure. Define the upper and lower
Lebesgue integrals, respectively, as
I*(f)L = inf{If I*(f)L = I*(f)L the function f is called Lebesgue integrable over E and the Lebesgue integral of f over E is denoted by
| |
| Examples 7.4.6: Lebesgue Integral for Bounded Functions | |
| |
Now a function f can be integrated (if it is integrable) using either the Riemann or the Lebesgue integral. Fortunately, for many simple functions the two integrals agree and the Lebesgue integral is indeed a generalization of the Riemann integral.
| Theorem 7.4.7: Riemann implies Lebesgue Integrable | |
If f is a bounded function defined on [a, b] such
that f is Riemann integrable, then f is Lebesgue
integrable and
| |
For most practial applications this theorem is all that is necessary: for continuous functions or bounded functions with at most countably many discontinuities over intervals [a, b] there is no need to distinguish between the Lebesgue or Riemann integral. All integration techniques we learned apply equally well, using either integral. But for more complicated situations or more theoretical purposes the Lebesgue integral is more useful, but then techniques such as integration by parts or substitution may no longer apply.
| Example 7.4.8: Riemann implies Lebesgue Integrable | |
| |
The Lebesgue integral has properties similar to those of the Riemann integral, but it is "more forgiving": you can change a function on a set of measure zero without changing the integral at all.
| Proposition 7.4.9: Properties of the Lebesgue Integral | |
Suppose f and g are two bounded, Lebesgue integrable
functions defined on a measurable set E with finite measure. Then:
| |
| Examples 7.4.10: Properties of the Lebesgue Integral | |
| |
At this point we could stop: we have extended the concept of integration to (bounded) functions defined on general sets (measurable sets with finite measure) without using partitions (subintervals). The new concept, the Lebesgue integral, agrees with the old one, Riemann integral, when both apply, and it removes some of the oddities mentioned before.
| Examples 7.4.11: Lebesgue is more general than Riemann | |
| |
But as the astute reader has surely already noticed, we have restricted our definition of Lebesque integrable function to bounded functions only. Can we continue to generalize the Lebesgue integral to functions that are unbounded, including functions that may occasionally be equal to infinity? To do that, we first need to define the concept of a measurable function.
| Definition 7.4.12: Measurable Function | |
Let f be a function from
E 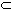 R
into
R R
into
R 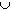 { -
{ -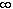 , , 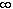 }
. The function f is called (Lebesgue) measurable if }
. The function f is called (Lebesgue) measurable if
| |
In other words, functions whose values are real numbers or possibly plus or
minus infinity are measurable if the inverse image of every interval
(-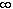 , a) is measurable.
, a) is measurable.
That is somewhat comparable to one of the equivalent definitions of continuous functions: a function f is continuous if the inverse image of every open interval is open. However, not every measurable function is continuous, while every continuous function is clearly measurable.
| Example 7.4.13: Measurable Functions | |
| |
Measurable functions that are bounded are equivalent to Lebesgue integrable functions.
| Proposition 7.4.14: Bounded Measurable Functions are Integrable | |
| If f is a bounded function defined on a measurable set E with finite measure. Then f is measurable if and only if f is Lebesgue integrable. | |
Measurable functions do not have to be continuous, they may be unbounded and they can, in particular, be equal to plus or minus infinity. On the other hand, measurable functions are "almost" continous.
| Proposition 7.4.15: Measurable Functions are Almost Continuous | |
Suppose f is a measurable function defined on an interval
[a, b] such that the set where f is plus or minus
infinity has measure zero. Then, for any  > 0
we can find a step function g and a continuous function h
such that > 0
we can find a step function g and a continuous function h
such that
| f(x) - g(x) | <except on a set of measure less than  . .
| |
Using measurable functions allows us to extend the Lebesgue integral first to non-negative functions that are not necessarily bounded and then to general measurable functions.
| Definition 7.4.16: Lebesgue Integral of Non-Negative Functions | |
If f is a measurable function defined on E and
h is a bounded measurable function such that
m( {x: h(x) # 0} ) is finite, then we define
If 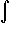 E f(x) dx
is finite, then f is called Lebesgue integrable over E. E f(x) dx
is finite, then f is called Lebesgue integrable over E.
| |
| Examples 7.4.17: Lebesgue Integral of Non-Negative Function | |
| |
The final step to define the Lebesgue integral of a general function is now easy.
| Definition 7.4.18: The General Lebesgue Integral | |
Let f be a measurable function and define the positive and
negative parts of f, respectively, as:
f +(x) = max(f(x), 0)so that f = f + - f -. Then f is Lebesgue integral if f + and f - are Lebesgue integrable and
| |
Proposition 7.4.X remains true for general Lebegues integrable functions.
| Examples 7.4.19: The General Lebesgue Integral | |
Suppose that f is an integrable function over a set E,
and take any  > 0. Show that > 0. Show that
| |
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 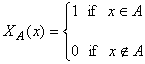
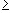 f }
f } f }
f }
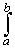 f(x) dx =
f(x) dx =