Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Example 7.4.7(d): Riemann implies Lebesgue Integrable

Show that the restriction of a bounded continuous function to a measurable set is Lebesgue integrable.
We should rephrase the question slightly so that it makes sense: suppose f is a bounded continuous function over an interval (a, b) and A is a measurable subset of (a, b) with finite measure. Then f is Lebesgue integrable over A.

First note that if [c, d) is an interval contained in (a, b) then the set f -1 ([c, d)) is measurable, because:

[c, d) = (c-1/n, d)
and
f -1 ([c, d)) = f -1 ( (c-1/n, d)) = f -1 ((c-1/n, d))
Since f is continuous, each set f -1 ((c-1/n, d)) is open, hence measurable, and the intersection of measurable sets is again measurable.

Now suppose f is bounded by M and fix an integer n. Define the sets

Ej = { x (a, b): (j-1)M/n f(x) < jM/n } A =
      = f -1 ( [(j-1)M/n, jM/n) ) A
where -n j n. Because of above each set Ej is measurable. Now the proof can continue just as in a previous exercise, so we will only sketch it here.

First: Define functions

sn(x) = M/n (j-1) XEj(x)
Sn(x) = M/n j XEj(x)
where the sum is taken from j = -n to n. Then the sets Ej are measurable, disjoint, and their union is A, and the functions sn and Sn are simple and integrable.

Second: Verify that

(1) sn(x) f(x) Sn(x)

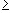
(2) I*(f)L Sn(x) dx and I*(f)L sn(x) dx

(3) I*(f)L - I*(f)L M/n m(A)

Third: Finish the proof.
Next | Previous | Glossary | Map | Discussion