Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Example 7.4.6(a): Lebesgue Integral for Bounded Functions

Is the function f(x) = x Lebesgue integrable over [0, 1]? If so, find the integral.
We have shown before that the function f(x) = x2 is Riemann integrable. Since step functions are special cases of simple functions, we could try to replicate that proof here, suitably modified for the function f(x) = x. But using simple functions instead of step functions actually simplifies the proof, so here we go.

We know that | f(x) | 1 over the interval [0, 1]. Define sets:

E1 = { x [0, 1]: 0 f(x) < 1/n }
E2 = { x [0, 1]: 1/n f(x) < 2/n }
E3 = { x [0, 1]: 2/n f(x) < 3/n }
...
Ej = { x [0, 1]: (j-1)/n f(x) < j/n}
for j = 1, 2, ..., n. Because f is continuous, the sets Ej are measurable (really - why?), they are disjoint, and their union (over the j's) equals [0, 1] (actually, the union equals [0, 1), but that does not matter - why?).

Now define two simple functions

Sn(x) = j/n XEj(x)
sn(x) = (j-1)/n XEj(x)
Fix an integer n and take a number x in [0, 1). Then x must be contained in exactly one set Ej, and on that set we have
sn(x) = (j-1)/n f(x) < j/n = Sn(x)
Therefore, on all of [0, 1], we know that
sn(x) f(x) Sn(x)
But then
I*(f)L Sn(x) dx = 1/n j m(Ej)
I*(f)L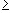 sn(x) dx = 1/n (j-1) m(Ej)
Therefore
I*(f)L - I*(f)L 1/n (j - (j-1)) m(Ej) =
      = 1/n m(Ej) = 1/n m([0, 1]) = 1/n
Since n was arbitrary the upper and lower Lebesgue integrals must agree, hence the function f is integrable.

Note that - with a few simple modifications - this proof could show that every bounded function f which has the property that the sets Ej are measurable is Lebesgue integrable.

It remains, though, to find the actual value of the integral. But we can easily compute the measure of the sets Ej using the fact that f(x) = x: for a fixed n we have

m( Ej ) = m({ x [0, 1]: (j-1)/n f(x) < j/n}) =
      = m({ x [0, 1]: (j-1)/n x < j/n}) =
      = m( [(j-1)/n, j/n] ) = 1/n
From the above computation it follows that
f(x) dx = lim 1/n j m(Ej) =
      = lim 1/n j 1/n = = lim 1/n2 j =
      = lim 1/n2 1/2 n (n-1) = 1/2
which is, incidentally, the same value as for the Riemann integral.
Next | Previous | Glossary | Map | Discussion