7.2. Integration Techniques
Why these ads ...
This section provides integration techniques, i.e. methods for finding
the actual value of an integral. We have already found the most basic
technique (the Integral Evaluation Shortcut or First Fundamental
Theorem of Calculus): to evaluate an integral over an interval
[a, b], find an antiderivate F of the integrand
f and compute F(b) - F(a).
Not all functions have a simple antiderivative, and any two antiderivatives
of the same function can differ only by a constant (prove this). But
different from finding a derivative, where a couple of rules can be used to
find virtually every derivative, finding an antiderivative is basically
a guessing game.
As is typical for finding the antiderivatives, the answers for the above examples
can not be deduced. They must be guessed, or learned. However, there are two standard
mechanisms that can be useful: substitution and integration by parts.
| Theorem 7.2.3: Substitution Rule |
| |
If f is a continuous function defined on [a, b], and
s a continuously differentiable function from [c, d] into
[a, b]. Then
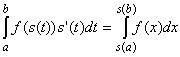
Proof
|
This theorem, in words, says that if you can identify a composition of functions
as well as the derivative of one of the composed functions, there's a good chance
you can find the antiderivative and evaluate the corresponding integral.
Think about the substitution rule as a "change of variable": if a particular
expression in x makes an integrand difficult, change it to
u. Then compute the derivative of u, i.e.
du/dx = u'(x) and "solve" it for du:
du = u'(x) dx. If you can use u'(x) dx to change
the integrand into an expression involving only u and no
x, then the substitution worked (and has hopefully simplified
the integrand). Otherwise try a different substitution or a
different technique altogether.
| Example 7.2.4: Applying the Substitution Rule |
| |
 Here is a simple example: find
Here is a simple example: find
 (4x + 3)2 dx (4x + 3)2 dx
 If F(x) is an antiderivative of f(x), find
If F(x) is an antiderivative of f(x), find
 f(cx + d) dx f(cx + d) dx
 x f(cx2) dx x f(cx2) dx
 f'(x) / f(x) dx f'(x) / f(x) dx
 Compute the area of a circle with radius r.
Compute the area of a circle with radius r.
 Find
Find
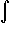 tan(x) dx
and tan(x) dx
and
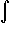 cot(x) dx cot(x) dx
 Find
Find
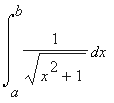 and
and
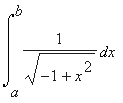
|
Another theorem that is commonly used is "integration by parts".
In order for integration by parts to be useful, three conditions should be
satisfied:
- The integrand must be a product of two expressions (one of which could
be 1)
- You must know the antiderivative of one of the two expressions
- The derivative of the other expression should become easier
Integration by parts can also be used to prove more interesting facts that
we might need later.
Integration by parts can be used to provide an effective means to compute
the value of an integral numerically. Of course, Riemann sums can be used
to approximate an integral, but convergence is usually slow. A much
faster convergence scheme is based on the trapezoid rule. To prove it,
we need the Mean Value Theorem for Integration:
Now we can state and prove the Trapezoid Rule.
The Trapezoid Rule is useful because the error
R(n) depends on
the square of
h. If
h is small,
h2
is a lot smaller so that the Trapezoid Rule provides a good approximation
to the numeric value of an integral (as long as
f is twice
continuously differentiable).
Our final integration technique uses
partial fraction decomposition
of a polynomial to simplify rational functions so that they can be integrated.
This theorem sounds complicated, so we should restate it in a more useful form:
- p(x) is a polynomial that can be factored into polynomials
qj
- each qj can not be factored any further (with
real coefficients)
- s(x) is another polynomial whose factors, if any, do not
cancel any of the qj, and whose degree is less than
the degree of p
- Then s(x)/p(x) can be written as a finite sum of simple
rational functions whose denominators consist of the qj's
and whose numerators have degree at most j-1
- finding the rj amounts to solving a system of
linear equations, as the examples will show
Several of the assumptions are technical:
- If the degree of s is greater than or equal to the degree
of p, then you can split s(x) / p(x) using long
division, and the remainder will be of the form where the theorem applies.
- If s does have factors in common with p, first
cancel out those factors, then apply the theorem to the resulting rational
function
The next examples will show how partial fraction decomposition can be used
to integrate rational functions whose denominator can be factored.
| Example 7.2.12: Integrating Rational Functions |
| | To compute the following integrals, use partial fraction
decomposition to write the rational function as a sum of simple rational
functions.
 Find the integral
Find the integral
 (1 - x2)-1 dx
where the interval [a, b] does not include 1 and -1. (1 - x2)-1 dx
where the interval [a, b] does not include 1 and -1.
 Find the integral
Find the integral
 (1 - x4)-1 dx (1 - x4)-1 dx
 Find the integral
Find the integral
 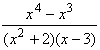 dx dx
|
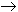 R
is a continuously differentiable function. Show that:
R
is a continuously differentiable function. Show that:
 0,
then there exists a number c
0,
then there exists a number c  [a, b]
with
[a, b]
with
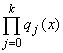 , where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
, where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  xr dx
xr dx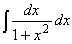
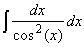
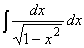
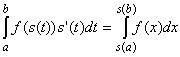
 (4x + 3)2 dx
(4x + 3)2 dx
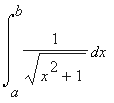 and
and
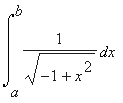
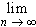
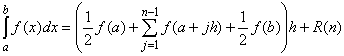
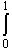 sin(x) cos(x) dx
sin(x) cos(x) dx
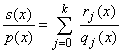
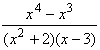 dx
dx