Example 7.2.7: Integration by Parts and Limits
Suppose f:[a, b] 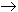 R
is a continuously differentiable function. Show that:
R
is a continuously differentiable function. Show that:
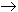 R
is a continuously differentiable function. Show that:
R
is a continuously differentiable function. Show that:
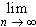
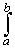 f(x) sin(nx) dx = 0
f(x) sin(nx) dx = 0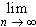
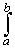 f(x) cos(nx) dx = 0
f(x) cos(nx) dx = 0
We already mentioned that this will be an application of integration by parts. Let's focus on the first statement and let g'(x) = sin(nx), where g' is the function in the Integration by Parts theorem. Then:
f(x) sin(n x) dx = - 1/n cos(nx) f(x) + 1/n
f'(x) cos(nx) dx
But
|sin(nx)|  1 and
|cos(nx)|
1 and
|cos(nx)|  1, and since both
f and f' are continuous functions on a closed,
bounded interval there are constants K and L such that
|f(x)|
1, and since both
f and f' are continuous functions on a closed,
bounded interval there are constants K and L such that
|f(x)|  K and
|f'(x)|
K and
|f'(x)|  L. Putting everything
together we get:
L. Putting everything
together we get:
|f(x) sin(n x) dx |
K/n + L(b-a)/n
Thus,
The proof of the second statement is left as an exercise.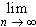
f(x) sin(n x) dx = 0
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of