4.1. Series and Convergence
Why these ads ...
So far we have learned about sequences of numbers. Now we will
investigate what may happen when we add all terms of a sequence
together to form what will be called an infinite series.
The old Greeks already wondered about this, and actually did not
have the tools to quite understand it This is illustrated by the
old tale of Achilles and the Tortoise.
| Example 4.1.1: Zeno's Paradox (Achilles and the Tortoise) |
| |
Achilles, a fast runner, was asked to race against a tortoise.
Achilles can run 10 meters per second, the tortoise only 5
meter per second. The track is 100 meters long. Achilles,
being a fair sportsman, gives the tortoise 10 meter advantage.
Who will win ?
|
- Both start running, with the tortoise being 10 meters ahead.
- After one second, Achilles has reached the spot where the tortoise started. The
tortoise, in turn, has run 5 meters.
- Achilles runs again and reaches the spot the tortoise has just been. The tortoise, in
turn, has run 2.5 meters.
- Achilles runs again to the spot where the tortoise has just been. The tortoise, in turn,
has run another 1.25 meters ahead.
This continues for a while, but whenever Achilles manages to reach the spot where the
tortoise has just been a split-second ago, the tortoise has again covered a little bit of
distance, and is still ahead of Achilles. Hence, as hard as he tries, Achilles only manages
to cut the remaining distance in half each time, implying, of course, that Achilles can
actually never reach the tortoise. So, the tortoise wins the race, which does not make
Achilles very happy at all.
 Obviously, this is not true, but where is the mistake ?
Obviously, this is not true, but where is the mistake ?
Now let's return to mathematics. Before we can deal with any new objects, we need to
define them:
| Definition 4.1.2: Series, Partial Sums, and Convergence |
| |
Let { a n } be an infinite sequence.
- The formal expression
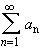 is called an (infinite) series.
is called an (infinite) series.
- For N = 1, 2, 3, ... the expression
lim Sn =
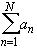 is called the N-th partial sum of the series.
is called the N-th partial sum of the series.
- If lim Sn exists and is finite, the
series is said to converge.
- If lim Sn does not exist or is
infinite, the series is said to diverge.
|
Note that while a series is the result of an infinite addition
- which we do not yet know how to handle - each partial sum is
the sum of finitely many terms only. Hence, the partial
sums form a sequence, and we already know how to deal with
sequences.
| Examples 4.1.3: |
| |
.gif) = 1/2 + 1/4 + 1/8 + 1/16 + ...
is an infinite series. The 3rd, 4th, and 5th partial sums, for example, are, respectively:
0.875, 0.9375, and 0.96875. = 1/2 + 1/4 + 1/8 + 1/16 + ...
is an infinite series. The 3rd, 4th, and 5th partial sums, for example, are, respectively:
0.875, 0.9375, and 0.96875.
-
 Does this series converge or diverge ?
Does this series converge or diverge ?
-
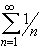 =
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is another infinite series,
called harmonic series. The 3rd, 4th, and 5th partial sums are,
respectively: 1.833, 2.0833, and 2.2833. =
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is another infinite series,
called harmonic series. The 3rd, 4th, and 5th partial sums are,
respectively: 1.833, 2.0833, and 2.2833.
-
 Does this series converge or diverge ?
Does this series converge or diverge ?
|
Actually, if a series contains positive and negative terms, many
of them may cancel out when being added together. Hence, there
are different modes of convergence: one mode that applies to
series with positive terms, and another mode that applies to
series whose terms may be negative and positive.
Conditionally convergent sequences are rather difficult to work
with. Several operations that one would expect to be true do not
hold for such series. The perhaps most striking example is the
associative law. Since
a + b = b + a for any two real
numbers
a and
b, positive or negative, one would
expect also that changing the order of summation in a series
should have little effect on the outcome. However:
| Theorem 4.1.6: Absolute Convergence and Rearrangement |
| |
Let
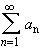 be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
Let
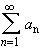 be a conditionally convergent series. Then, for any real number
c there is a rearrangement of the series such that the
new resulting series will converge to c.
be a conditionally convergent series. Then, for any real number
c there is a rearrangement of the series such that the
new resulting series will converge to c.
Proof
|
It seems that conditionally convergent series contain a few
surprises. As a concrete example, we can rearrange the alternating
harmonic series so that it converges to, say, 2.
| Examples 4.1.7: Rearranging the Alternating Harmonic Series |
| |
 Find a rearrangement of the alternating harmonic series
Find a rearrangement of the alternating harmonic series
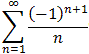 that is within 0.001 of 2, i.e. show a concrete rearrangement of that
series that is about to converge to the number 2.
that is within 0.001 of 2, i.e. show a concrete rearrangement of that
series that is about to converge to the number 2.
 Find a rearrangement of the alternating harmonic series
Find a rearrangement of the alternating harmonic series
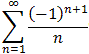 that diverges to positive infinity.
that diverges to positive infinity.
|
We will give one more rather abstract result on series before
concluding this chapter as we started it, with a story. The one
result that is of more theoretical importance is
Our final story is frequently called the "Leaning Tower of Lire".
While the introductory story about Achilles and the Tortoise introduces an
apparent paradox which we were able to resolve using a convergent (geometric)
series, this story uses the properties of a divergent (harmonic) series to shed
light on an unbelievable but true situation.
| Example 4.1.10: The Leaning Tower of Lire |
| |
 Jillian, a diligent but overworked student, fell asleep in the library and
got locked in for the night. When she awoke, the room was dimly lit and she
was alone. To pass the time (and to annoy the librarian in the morning) she
decided to stack books on a table so that they would overhang the edge
of the table.
Jillian, a diligent but overworked student, fell asleep in the library and
got locked in for the night. When she awoke, the room was dimly lit and she
was alone. To pass the time (and to annoy the librarian in the morning) she
decided to stack books on a table so that they would overhang the edge
of the table.
Assuming she has an unlimited supply of books, all of equal width 2 and
weight 1 (say), what is the biggest overhang she can produce? To make it
more interesting, let's say she can use only one book at each level.
|
But our story-time is over - the next section introduces convenient tests to
determine quickly and efficiently whether a series converges or diverges.
![]() Obviously, this is not true, but where is the mistake ?
Obviously, this is not true, but where is the mistake ?
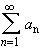 converges absolutely if the sum of the absolute values
converges absolutely if the sum of the absolute values
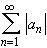 converges.
converges.
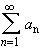 be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
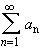 and
and
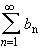 be two absolutely convergent series. Then:
be two absolutely convergent series. Then:
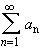 converges if and only if for every
converges if and only if for every
 > 0 there is a positive
integer N such that if m > n > N then
> 0 there is a positive
integer N such that if m > n > N then
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 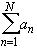 is called the N-th partial sum of the series.
is called the N-th partial sum of the series.
.gif) = 1/2 + 1/4 + 1/8 + 1/16 + ...
is an infinite series. The 3rd, 4th, and 5th partial sums, for example, are, respectively:
0.875, 0.9375, and 0.96875.
= 1/2 + 1/4 + 1/8 + 1/16 + ...
is an infinite series. The 3rd, 4th, and 5th partial sums, for example, are, respectively:
0.875, 0.9375, and 0.96875.
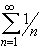 =
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is
=
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is 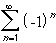 converge absolutely, conditionally, or not at all ?
converge absolutely, conditionally, or not at all ?
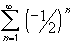 converge absolutely, conditionally, or not at all ?
converge absolutely, conditionally, or not at all ?
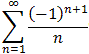 converge absolutely, conditionally, or not at all (this series
is called alternating harmonic series) ?
converge absolutely, conditionally, or not at all (this series
is called alternating harmonic series) ?
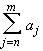 | <
| <