Examples 4.1.7(b):
Take a look at the following inequality:2n + j < 2n+1for j = 1, 3, ..., 2n-1 (which makes for 2n-1 terms). Therefore:
(2n + 1)-1 + (2n + 3)-1 + ... + (2n+1 - 1)-1 > 2n-1 / 2n+1 = 1/4But now we can rearrange the terms of the alternating harmonic series as follows:
1 - 1/2 + 1/3 - 1/4 +Since each term in square brackets is greater than 1/4 - 1/6 the rearranged series must diverge to positive infinity.
[ ( 1/5 + 1/7 ) - 1/6 ] +
[ ( 1/9 + 1/11 + 1/13 + 1/15 ) - 1/8 ] + ...
+ [ ( (2n+1)-1 + (2n+3)-1 + ... + (2n+1-1)-1 ) - 1/2n+2 ] + ...

 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 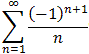 that diverges to positive infinity.
that diverges to positive infinity.