Theorem 4.1.11: Cauchy Product
Let 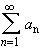 and
and
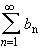 be two absolutely convergent series. Define
be two absolutely convergent series. Define
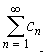 is absolutely convergent and
is absolutely convergent and
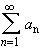 and
and
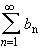 be two absolutely convergent series. Define
be two absolutely convergent series. Define
cn =Then the series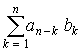
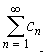 is absolutely convergent and
is absolutely convergent and
=
*
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of