Interactive Real Analysis
- part of Examples 4.1.7(a): Rearranging the Alternating Harmonic Series
Find a rearrangement of the alternating harmonic series
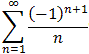that is within 0.001 of 2, i.e. show a concrete rearrangement of that
series that is about to converge to the number 2.
Back
This is a simple numeric computation, involving some trial and error.
First, let's collect positive odd terms so that they add up to something
larger than 2:
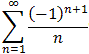that is within 0.001 of 2, i.e. show a concrete rearrangement of that
series that is about to converge to the number 2.
Back1 + 1/3 + ... + 1/15 = 2.021800422Next we subtract the first negative term:
1 + 1/3 + ... + 1/15Then we again add positive terms until we are larger than 2 again:
- 1/2
= 1.521800422
1 + 1/3 + ... + 1/15Subtracting the next negative term gives:
- 1/2
+ 1/17 + 1/19 + ... + 1/41
= 2.004063454
1 + 1/3 + ... + 1/15Again adding positive terms:
- 1/2
+ 1/17 + 1/19 + ... + 1/41
- 1/4
= 1.754063454
1 + 1/3 + ... + 1/15Once again we subtract the next negative term:
- 1/2
+ 1/17 + 1/19 + ... + 1/41
- 1/4
+ 1/43 + 1/45 + ... + 1/69
= 2.009446048
1 + 1/3 + ... + 1/15and add positive terms:
- 1/2
+ 1/17 + 1/19 + ... + 1/41
- 1/4
+ 1/43 + 1/45 + ... + 1/69
- 1/6
= 1.842779381
1 + 1/3 + ... + 1/15Now we are within 0.001 of 2, and it seems clear how we can continue in this matter to find a rearrangement of the alternating harmonic series that converges to 2.
- 1/2
+ 1/17 + 1/19 + ... + 1/41
- 1/4
+ 1/43 + 1/45 + ... + 1/69
- 1/6
+ 1/71 + 1/73 + ... + 1/95
= 2.000697893