Example 7.2.4(b): Applying the Substitution Rule
Why these ads ...
If
F(x) is an antiderivative of
f(x), find:
 f(cx + d) dx
f(cx + d) dx
 x f(cx2) dx
x f(cx2) dx
 f'(x) / f(x) dx
f'(x) / f(x) dx
Back
To find
 f(cx + d) dx
f(cx + d) dx
we make the substitution
u = cx + d so that
du/dx = c, or du = c dx
Therefore
 f(cx + d) dx =
f(cx + d) dx =
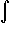 f(u) dx =
f(u) dx =
= 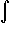 1/c f(u) c dx =
1/c
1/c f(u) c dx =
1/c 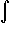 f(u) du =
f(u) du =
= 1/c [F(u(b)) - F(u(a))] = 1/c [F(cb + d) - F(ca + d)]
To find
 x f(cx2) dx
x f(cx2) dx
we make the substitution
u = cx2 so that
du/dx = 2cx or du = 2cx dx
Therefore
 x f(cx2) dx =
x f(cx2) dx =
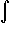 x f(u) dx =
x f(u) dx =
= 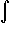 1/2c f(u) 2cx dx =
1/2c f(u) 2cx dx =
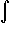 1/2c f(u) du =
1/2c f(u) du =
= 1/2c [ F(u(b)) - F(u(a)) ] =
= 1/2c [ F(cb2) - F(ca2) ]
To find
 f'(x) / f(x) dx
f'(x) / f(x) dx
we make the substitution
u = f(x) so that
du/dx = f'(x), or du = f'(x) dx
Therefore
 f'(x) / f(x) dx =
f'(x) / f(x) dx =
 1/ f(x) f'(x) dx =
1/ f(x) f'(x) dx =
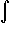 1/u du =
1/u du =
= ln(|f(b)|) - ln(|f(a)|)
 f(cx + d) dx
we make the substitution
f(cx + d) dx
we make the substitution
f(cx + d) dx =
f(u) dx =
1/c f(u) c dx = 1/c
f(u) du =
 x f(cx2) dx
we make the substitution
x f(cx2) dx
we make the substitution
x f(cx2) dx =
x f(u) dx =
1/2c f(u) 2cx dx =
1/2c f(u) du =
 f'(x) / f(x) dx
we make the substitution
f'(x) / f(x) dx
we make the substitution
f'(x) / f(x) dx =
1/ f(x) f'(x) dx =
1/u du =
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of