Proposition 7.2.9: The Trapezoid Rule
Let f be a twice continuously differentiable function defined
on [a, b] and set
We first prove a simpler version of the trapezoid rule using the Mean Value
Theorem for integrals and integration by parts.
K = sup{ |f''(x) |, xIf h = (b - a) / n, where n is a positive integer, then[a, b] }
where |R(n)| < K/12 (b-a) h2.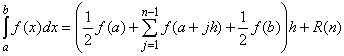
Simple Trapezoid Rule: Let f be a function defined on the interval [0, 1]
so that f is twice continuously differentiable. Then there
exists a number c 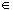 [0, 1] so
that
[0, 1] so
that
The trick to prove this statement is to define a function
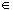 [0, 1] so
that
[0, 1] so
that
f(x) dx = 1/2 (f(0) + f(1)) - 1/12 f''(c)
v(x) = 1/2 x (1 - x)which has the properties:
|
Using integration by parts with g'(x) = v''(x) we get:f(x) dx = -
v''(x) f(x) dx
Again using integration by parts with g'(x) = v'(x) we get:v''(x) f(x) dx = v'(1) f(1) - v'(0) f(0) -
v'(x) f'(x) dx =
= -1/2 f(1) - 1/2 f(0) -v'(x) f'(x) dx
where we used the Mean Value Theorem for Integration with some number c inside the interval [0, 1]. Taking everything together (careful with the negative signs) we then have:v'(x) f'(x) dx = v(1) f'(1) - v(0) f'(0) -
v(x) f''(x) dx =
-v(x) f''(x) dx =
- f''(c)v(x) dx = - f''(c) 1/12
which proves the simple Trapezoid Rule.f(x) dx = 1/2 f(1) + 1/2 f(0) +
v'(x) f'(x) dx =
= 1/2 f(1) + 1/2 f(0) - 1/12 f''(c)
To prove the general Trapezoid Rule, assume that f is defined
on [a, b]. Let h = (b - a) / n, pick an integer
j, and define the function
u(x) = a + jh + xh for x 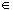 [0, 1].
The composite function g(x) = f(u(x)) is twice continuously differentiable
and defined on the interval [0, 1] so that the simple trapezoid rule
applies:
[0, 1].
The composite function g(x) = f(u(x)) is twice continuously differentiable
and defined on the interval [0, 1] so that the simple trapezoid rule
applies:
But g(0) = f(u(0)) = f(a +jh), g(1) = f(u(1)) = f(a + (j+1)h), and g''(x) = h2 f''(x). Moreoverg(x) dx = 1/2 g(0) + 1/2 g(1) - 1/12 g''(c)
1/2 g(0) + 1/2 g(1) - 1/12 g''(c) =Therefore:g(x) dx =
f(u(x)) dx =
= 1/hf(u(x)) u'(x) dx = 1/h
f(u) du
Summing this equation from j = 0 to j = n-1 gives: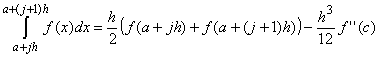
where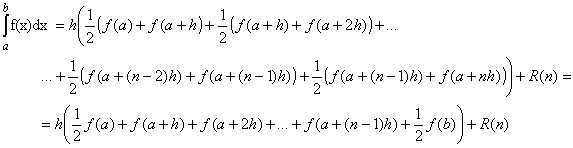
which finishes the proof.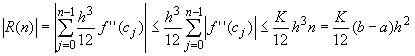
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  0 for all
x
0 for all
x