Theorem 7.2.11: Partial Fraction Decomposition
Suppose p(x) is a polynomial of degree n
such that p(x) = 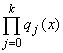 , where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
, where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
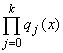 , where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
, where
each qj is polynomial of degree j that
is irreducible over R. If s(x) is another polynomial
of degree less than n with no factors in common with
p(x), then the rational function s(x) / p(x)
can be written as a finite sum
where each rj is a polynomial of degree less than j.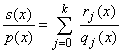
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of