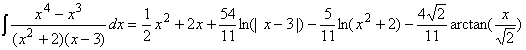Example 7.2.12(c): Integrating Rational Functions
Why these ads ...
Find the integral
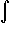
 dx
dx
Back
This time it seems that we can not use partial fraction decomposition because
the degree of the numerator is higher than that of the denominator. To
remedy that problem, we use "long division" to divide the polynomials:
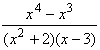 = x + 2 +
= x + 2 + 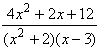
Integrating
x + 2 is easy, so the problem is reduced to finding
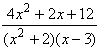 dx
dx
and the partial fractions decomposition theorem applies just fine to this
integrand. We know that
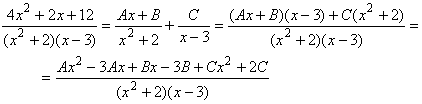
Therefore we get three equations in three unknowns:
| -3B + 2C = 12 | (for the constant coefficient) |
| -3A + B = 2 | (for the x coefficient) |
| A + C = 4 | (for the x2 coefficient) |
Solving this system of equations gives
A = -10/11, B = -8/11, C = 54/11
Therefore the one complicated integral above changes into three simpler ones:
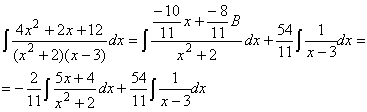
The second integral is easy (involving the
ln). The first integral
seems to be somewhat difficult, because
 arctan(x) = 1 / (1 + x2)
arctan(x) = 1 / (1 + x2)
which does not quite work, and the numerator is
not the derivative of the
denominator, so the
ln is out, too. But a little algebra and some
substitution will do the trick:
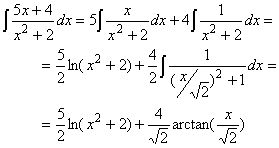
Taking everything together gives:
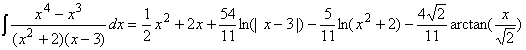
= x + 2 +
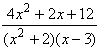
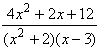 dx
and the partial fractions decomposition theorem applies just fine to this
integrand. We know that
dx
and the partial fractions decomposition theorem applies just fine to this
integrand. We know that
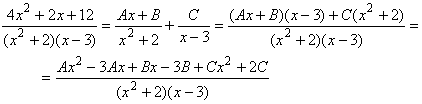
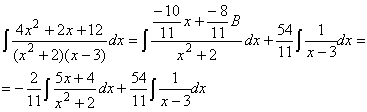
 arctan(x) = 1 / (1 + x2)
which does not quite work, and the numerator is not the derivative of the
denominator, so the ln is out, too. But a little algebra and some
substitution will do the trick:
arctan(x) = 1 / (1 + x2)
which does not quite work, and the numerator is not the derivative of the
denominator, so the ln is out, too. But a little algebra and some
substitution will do the trick:
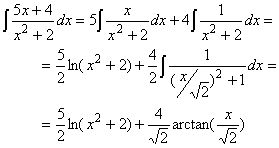
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of