Example 7.2.10: Application of the Trapezoid Rule
Why these ads ...
Compare the numeric approximations to the integral
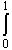 sin(x) cos(x) dx
sin(x) cos(x) dx
obtained by using (a) a left Riemann sum and (b) the Trapezoid Rule, using
a partition of size 5 and of size 100.
Back
First, let's determine the exact value of the integral by substitution. Let
u = sin(x) so that
du/dx = cos(x) or du = cos(x) dx
Then
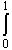 sin(x) cos(x) dx =
sin(x) cos(x) dx =
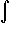 u du =
u du =
= 1/2 (sin2(1) - sin2(0)) = 0.5(0.7080734183 - 0) = 0.3540367092
To find the left Riemann sum, we let f(x) = sin(x) cos(x) and compute:
f(0) = 0
f(0.2) = 0.1947091712
f(0.4) = 0.3586780454
f(0.6) = 0.4660195430
f(0.8) = 0.4997868015
and therefore
|
|
R(P, f) = 1/5*(f(0) + f(0.2) + f(0.4) + f(0.6) + f(0.8)) =
= 0.2 * 1.519193562 = 0.3038387122
The error between the approximate and exact value is about 0.05, or 14%. To estimate
the error using the trapezoid rule, we compute
f''(x) = -4 sin(x) cos(x) so that
K = 4. Then
|R| < 4/12 * 1 * 0.22 = 0.04 / 3 = 0.013
so that even the theoretically worst error is a lot better (less than 4%). To find
the value using the trapezoid rule, we need to evaluate
f at the same
values as before and also compute
f(1) = 0.4546487134. Then the
trapezoid rule, combining these numbers a little different than the left
Riemann sum, gives:
[1/2 f(0) + f(0.2) + f(0.4) + f(0.6) + f(0.8) + 1/2 f(1)] * 0.2 =
= [0 + 1.519193562 + 0.5 * 0.4546487134 ] * 0.2 =
= 0.3493035838
which is indeed much closer than our previous approximation (the error is only about
1%).
|
|
Incidentally, if we increased the size of the partition to 100, the error
committed by the trapezoid rule would already be less than
1/3 * 0.012 = 0.00003 or 0.01%, whereas the left
Riemann sum still has an error of about 0.003, or about 1% (compare the
value of the applet with the exact value above).
|
sin(x) cos(x) dx
sin(x) cos(x) dx =
u du =
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of