MathCS.org - Real Analysis: Example 7.2.6(b): Applying Integration by Parts

Example 7.2.6(b): Applying Integration by Parts

Why these ads ...

Find 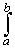x² cos(x) dx

Back

This time we define

g'(x) = cos(x) so that g(x) = 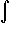cos(x) dx = sin(x)
f(x) = x² so that f'(x) = 2x

Then G(x) = f(x) g(x) = sin(x) x² and

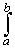x² cos(x) dx = G(b) - G(a) - 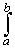2x sin(x) dx

Intergration by parts reduced the original problem to finding a slightly simpler integral, but we can not find the second integral immediately. What worked once might work again so let's use integration by parts on the second integral with:

g'(x) = sin(x) so that g(x) = 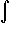sin(x) dx = -cos(x)
f(x) = 2x so that f'(x) = 2

so that G^*(x) = -2x cos(x). Therefore

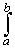2x sin(x) dx = G^*(b) - G^*(a) + 2 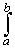cos(x) dx

Taking everything together we have:

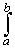x² cos(x) dx = G(b) - G(a) - [G^*(b) - G^*(a) + 2 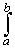cos(x) dx ] =
= G(b) - G(a) - G^*(b) + G^*(a) - 2 (sin(b) - sin(a)) =
= sin(b) b² - sin(a) a² + 2b cos(b) - 2a cos(a) -2sin(b) + 2sin(a)

Next | Previous | Glossary | Map | Discussion

Interactive Real Analysis - part of MathCS.org

Example 7.2.6(b): Applying Integration by Parts