Interactive Real Analysis
- part of Example 7.4.4(e): Lebesgue Integral for Simple Functions
We have seen before that the representation of a simple function is
not unique. Show that the Lebesgue integral of a simple function is independent
of its representation.
Context
We have to show that if s is a simple function with two
different representations, then the integrals using either representation
agree.
ContextFirst assume that there are two representations for s
sA(x) =such that sA(x) = sB(x). Let's assume that the integral of s using the first representation exists, i.e. the measure of all sets Aj is finite.aj XAj(x) with Aj disjoint and aj not zero
sB(x) =
If x 
Bk
then x must be contained in one of the Aj's
because otherwise sB(x) # 0 and sA(x) = 0.
Therefore
Bk
Aj so
that m(Bk) is finite for all
k so that sB is integrable.
By the same reasoning we have
Bk =If AjBk ) and Aj =
Bk
is not empty, then for
x
Aj
Bk
we have
aj = sA(x) = sB(x) = bkso that aj = bk in that case. Putting everything together gives:
so that the integrals agree regardless of the representation.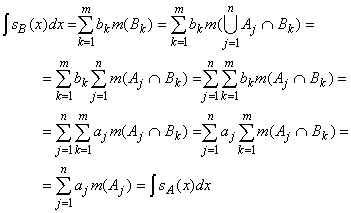
It remains to show that the integral of a simple function agrees with the integral over the canonical representation of that function, i.e. when the sets are disjoint and the coefficients are not zero.