Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Proposition 7.1.12: Properties of the Riemann Integral

Suppose f and g are Riemann integrable functions defined on [a, b]. Then
  1. c f(x) + d g(x) dx = c f(x) dx + d g(x) dx
  2. If a < c < b then f(x) dx = f(x) dx 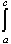+ f(x) dx
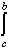  3. | f(x) dx | | f(x) | dx
  4. If g is another function defined on [a, b] such that g(x) < f(x) on [a, b], then g(x) dx f(x) dx
  5. If g is another Riemann integrable function on [a, b] then f(x) . g(x) is integrable on [a, b]

Proof:

Next | Previous | Glossary | Map | Discussion