Interactive Real Analysis
- part of Example 7.4.6(c): Lebesgue Integral for Bounded Functions
Is the Dirichlet function restricted to [0, 1] Lebesgue
integrable? If so, find the integral.
Context
The Dirichlet function restricted to [0, 1] is a simple function
and we have already seen that its integral is zero.
But we have now two definitions of the integral in case of a simple
function, and we need to show that both definitions agree.
Context
If
f(x) =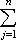 
cj XEj
is a simple function, then the infimum over the integrals
of all simple functions bigger than f must be smaller than the
integral of f, which is itself a simple function. In other
words, if f is a simple function than we have automatically
I*(f)LSimilarly we have
f(x) dx =
I*(f)LBut since I*(f)L
I*(f)L we have for every
simple function f that
so that for simple functions both definitions of the Lebesgue integral agree. In particular, the Lebesgue integral of the Dirichlet function over [0, 1] is then zero.