Example 7.4.4(d): Lebesgue Integral for Simple Functions
Define two simple functions
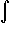 s1(x) dx =
s1(x) dx =
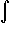 s2(x) dx.
s2(x) dx.
To show that s1(x) = s2(x) is easy:
s1(x) = 2 X[0, 2](x) + 4 X[1, 3](x)Show that s1(x) = s2(x) and
s2(x) = 2 X[0, 1)(x) + 6 X[1, 2](x) + 4 X(2, 3](x)
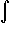 s1(x) dx =
s1(x) dx =
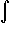 s2(x) dx.
s2(x) dx.
- Take x
 [0, 1): Then
s1(x) = 2 and
s2(x) = 2.
[0, 1): Then
s1(x) = 2 and
s2(x) = 2.
- Take x
 [1, 2]: Then
s1(x) = 2 + 4 = 6 and
s2(x) = 6.
[1, 2]: Then
s1(x) = 2 + 4 = 6 and
s2(x) = 6.
- Take x
 (2, 3]: Then
s1(x) = 4 and
s2(x) = 4.
(2, 3]: Then
s1(x) = 4 and
s2(x) = 4.
By definition we have:
ands1(x) dx = 2 m([0, 2]) + 4 m([1, 3]) = 4 + 8 = 12
so that the value of the integrals agree as well.s2(x) dx = 2 m([0, 1)) + 6 m([1, 2]) + 4 m((2, 3]) = 2 + 6 + 4 = 12
In other words, the value of the integral is independent of the representation of the simple functions in this example.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of