Proposition 6.4.1: Continuity and Topology
- f is continuous
- If D is open, then the inverse image of every open set under f is again open.
- If D is open, then the inverse image of every open interval under f is again open.
- If D is closed, then the inverse image of every closed set under f is again closed.
- If D is closed, then the inverse image of every closed interval under f is again closed.
- The inverse image of every open set under f is the intersection of D with an open set.
- The inverse image of every closed set under f is the intersection of D with a closed set.
Proof:
(1) => (2): Assume that f is continuous on an open set
D. Let U be an open set in the range of f. We need
to show that f-1(U)
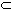 D is
again open. Take any x0
D is
again open. Take any x0
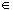 f-1(U).
That is equivalent to saying that f( x0)
f-1(U).
That is equivalent to saying that f( x0)
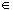 U.
Since U is open, we can find an
U.
Since U is open, we can find an  >
0 such that the
>
0 such that the  -
neighborhood of f( x0)
is contained in U. For this fixed
-
neighborhood of f( x0)
is contained in U. For this fixed  we
can use the continuity of f to pick a
we
can use the continuity of f to pick a  >
0 such that
>
0 such that
- if | x - x0|
<
 then |
f(x) - f( x0) |
<
then |
f(x) - f( x0) |
< 
This implies that the  -
neighborhood of x0is
contained in f-1(U).
Hence, the inverse image of the arbitrary set U is open.
-
neighborhood of x0is
contained in f-1(U).
Hence, the inverse image of the arbitrary set U is open.
(2) => (1): Assume that the inverse image f-1(U)
of every open set U is open. Take any point x0
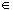 U and
pick an
U and
pick an  >
0. Then the
>
0. Then the  -
neighborhood of f( x0)
is an open set, so that it's inverse image is again open. That
inverse image contains x0,
and since it is open it contains a
-
neighborhood of f( x0)
is an open set, so that it's inverse image is again open. That
inverse image contains x0,
and since it is open it contains a  -
neighborhood of x0for
some
-
neighborhood of x0for
some  > 0.
But that is exactly what we want:
> 0.
But that is exactly what we want:
- if | x - x0|
<
 then this
set is contained in the set f-1(
f( x0) -
then this
set is contained in the set f-1(
f( x0) -  ,
f( x0) +
,
f( x0) +  )
)
or in other words
- if | x - x0|
<
 then |
f(x) - f( x0) |
<
then |
f(x) - f( x0) |
< 
(2) <=> (3): This follows immediately from the fact that every open set in the real line can be written as the countable union of open intervals.
(2) <=> (4): This follows immediately by looking at complements, i.e. from the fact that
- f-1( comp(U) ) = comp( f-1(U) )
That equality should be proved as an exercise.
(4) <=> (5): This follows again by combining the two previous remarks.
(6), (7): This proof is very similar to the proof of (2) <=> (1). In fact, where in that previous proof have we used the fact that the domain D of the function is open ? The details are left as an exercise again.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of