6.3. Discontinuous Functions
Why these ads ...
| Definition 6.3.1: Discontinuous function |
| |
If a function fails to be continuous at a point c, then the function is
called discontinuous at c, and c is called a point of
discontinuity, or simply a discontinuity.
|
Points of discontinuity can be classified into three different categories: 'fake'
discontinuities, 'regular' discontinuities, and 'difficult' discontinuities.
| Examples 6.3.2: |
| |
- Consider the following three functions:
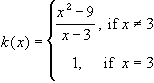
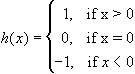
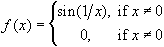
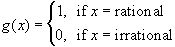
 Which of these functions, without proof, has a 'fake' discontinuity, a
'regular' discontinuity, or a 'difficult' discontinuity ?
Which of these functions, without proof, has a 'fake' discontinuity, a
'regular' discontinuity, or a 'difficult' discontinuity ?
|
Of course, we need some mathematical description of the various types of
discontinuities that a function could have.
| Definition 6.3.3: Classification of Discontinuities |
| |
Suppose f is a function with domain D and c
 D is a point of discontinuity of f. D is a point of discontinuity of f.
- if
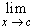 f(x) exists, then
c is called removable discontinuity. f(x) exists, then
c is called removable discontinuity.
- if
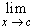 f(x) does not
exist, but both f(x) does not
exist, but both
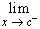 f(x) and f(x) and
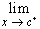 f(x) exit, then c is
called a discontinuity of the first kind , or jump discontinuity f(x) exit, then c is
called a discontinuity of the first kind , or jump discontinuity
- if either
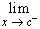 f(x) or f(x) or
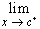 f(x) does not exist, then
c is called a discontinuity of the second kind, or essential discontinuity. f(x) does not exist, then
c is called a discontinuity of the second kind, or essential discontinuity.
|
| Examples 6.3.4: |
| |
- Consider the functions from the previous examples. Then
 Prove that k(x) has a removable discontinuity at x = 3, and draw the graph of k(x).
Prove that k(x) has a removable discontinuity at x = 3, and draw the graph of k(x).
 Prove that h(x) has a jump discontinuity at x = 0, and draw the graph of h(x)
Prove that h(x) has a jump discontinuity at x = 0, and draw the graph of h(x)
 Prove that f(x) has a discontinuity of second kind at x = 0
Prove that f(x) has a discontinuity of second kind at x = 0
 What kind of discontinuity does the function g(x) have at every point (with proof).
What kind of discontinuity does the function g(x) have at every point (with proof).
|
It is clear that any function is either continuous at any given point in its
domain, or it has a discontinuity of one of the above three kinds. It is also
clear that removable discontinuities are 'fake' ones, since one only has to
define f(c) =
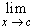
f(x)
and the function will be continuous at c. Of the other two types of discontinuities,
the one of second kind is hard. Fortunately, however, discontinuities of second
kind are rare, as the following results will indicate.
| Definition 6.3.5: Monotone Function |
| |
A function f is monotone increasing on (a, b) if f(x)
 f(y) whenever x < y. f(y) whenever x < y.
A function f is monotone decreasing on (a, b) if f(x)
 f(y) whenever x < y. f(y) whenever x < y.
A function f is called monotone on (a, b) if it is
either always monotone increasing or monotone decreasing.
|
Note that f is increasing if -f is decreasing, and visa versa. Equivalently, f is
increasing if
- f(x) / f(y)
 1 whenever x < y
1 whenever x < y
- f(x) - f(y)
 0 whenever x < y
0 whenever x < y
These inequalities are often easier to use in applications, since
their left sides take a very nice and simple form. Next, we will
determine what type of discontinuities monotone functions can
possibly have. The proof of the next theorem, despite its surprising
result, is not too bad.
| Theorem 6.3.6: Discontinuities of Monotone Functions |
| |
If f is a monotone function on an open interval (a, b), then
any discontinuity that f may have in this interval is of the first
kind.
If f is a monotone function on an interval [a, b], then f has at
most countably many discontinuities.
Proof
|
This theorem also states that if a function wants to have a discontinuity
of the second kind at a point
x = c, then it can not be monotone
in any neighborhood of
c.
In other words,
f must look pretty bad if it has a discontinuity of the
second kind.
| Examples 6.3.8: |
| |
 What kind of discontinuity does the function f(x) = exp(1/x) have at x = 0 ?
What kind of discontinuity does the function f(x) = exp(1/x) have at x = 0 ?
 What kind of discontinuity does the function f(x) = x sin(1/x) have at x = 0 ?
What kind of discontinuity does the function f(x) = x sin(1/x) have at x = 0 ?
 What kind of discontinuity does the function f(x) = cos(1/x) have at x = 0 ?
What kind of discontinuity does the function f(x) = cos(1/x) have at x = 0 ?
|
 D is a point of discontinuity of f.
D is a point of discontinuity of f.
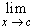 f(x)
and the function will be continuous at c. Of the other two types of discontinuities,
the one of second kind is hard. Fortunately, however, discontinuities of second
kind are rare, as the following results will indicate.
f(x)
and the function will be continuous at c. Of the other two types of discontinuities,
the one of second kind is hard. Fortunately, however, discontinuities of second
kind are rare, as the following results will indicate.
 f(y) whenever x < y.
f(y) whenever x < y.
 1 whenever x < y
1 whenever x < y
 0 whenever x < y
0 whenever x < y
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 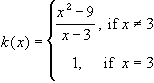
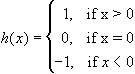
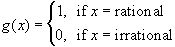
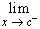 f(x) and
f(x) and
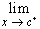 f(x) exit, then c is
called a discontinuity of the first kind , or jump discontinuity
f(x) exit, then c is
called a discontinuity of the first kind , or jump discontinuity
 f(y) whenever x < y.
f(y) whenever x < y.