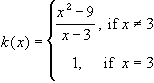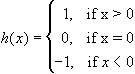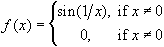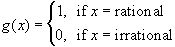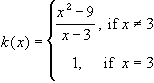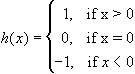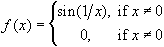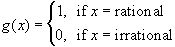Examples 6.3.2:
Why these ads ...
Which of the following functions, without proof, has a 'fake' discontinuity,
a 'regular' discontinuity, or a 'difficult' discontinuity ?
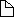
Back
|
|
|
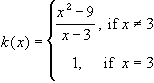
This function seems to have a 'fake' discontinuity at
x = 3, since
we could easily move the single point at
x = 3 to the right height,
thereby filling in the discontinuity.
|
|
|
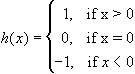
This function, while simple, seems to have a 'true' discontinuity
at
x = 0. We can not change the function at a single point to
make it continuous.
|
|
|
This function is unclear. It is hard to determine what exactly
is going on as
x gets closer to zero. Assuming that the function
does turn out to be discontinuous at
x = 0, it definitely seems
to have a 'difficult' discontinuity at x = 0.
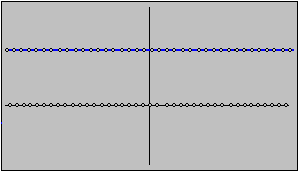
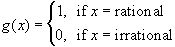
This function is impossible to graph. The picture above is only
a poor representation of the true graph. Nonetheless, given any
point
x, the function jumps between 1 and 0 in every neighborhood
of
x. That seems to mean that the function has a difficult discontinuity
at every point.
Interactive Real Analysis
- part of