6.2. Continuous Functions
Why these ads ...
If one looks up
continuity in a thesaurus, one finds synonyms
like
perpetuity or
lack of interruption. Descartes
said that a function is continuous if its graph can be drawn without
lifting the pencil from the paper.
| Example 6.2.1: |
| |
 Use the above imprecise meaning of continuity to decide which of the two
functions are continuous:
Use the above imprecise meaning of continuity to decide which of the two
functions are continuous:
- f(x) = 1 if x > 0 and f(x) = -1 if
x < 0. Is this function continuous ?
- f(x) = 5x - 6. Is this function continuous?
|
However, if we want to deal with more complicated functions, we
need mathematical concepts that we can manipulate.

This, like many
epsilon-delta definitions and arguments, is
not easy to understand. Click on the
Java icon to see an
applet that tries to illustrate the definition.
Continuous functions are precisely those groups of functions that
preserve limits, as the next proposition indicates:
| Proposition 6.2.3: Continuity preserves Limits |
| |
If f is continuous at a point c in the domain
D, and { xn } is a sequence of points in
D converging to c, then
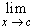 f(x) = f(c). f(x) = f(c).
If
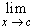 f(x) = f(c)
for every sequence { xn } of points in D
converging to c, then f is continuous at the point c. f(x) = f(c)
for every sequence { xn } of points in D
converging to c, then f is continuous at the point c.
Proof
|
Again, as with limits, this proposition gives us two equivalent
mathematical conditions for a function to be continuous, and either
one can be used in a particular situation.
| Example 6.2.4: |
| |
-
 Which of the following two functions is continuous:
Which of the following two functions is continuous:
- If f(x) = 5x - 6, prove that f is continuous in its
domain.
- If f(x) = 1 if x is rational and f(x) = 0 if
x is irrational, prove that x is not continuous at any
point of its domain.
-
 If f(x) = x if x is rational and f(x) = 0 if
x is irrational, prove that f is continuous at 0.
If f(x) = x if x is rational and f(x) = 0 if
x is irrational, prove that f is continuous at 0.
-
 If f(x) is continuous in a domain D, and
{ xn }
is a Cauchy sequence in D, is the sequence
{ f ( xn ) }
also Cauchy ?
If f(x) is continuous in a domain D, and
{ xn }
is a Cauchy sequence in D, is the sequence
{ f ( xn ) }
also Cauchy ?
|
Continuous functions can be added, multiplied, divided, and composed
with one another and yield again continuous functions.
| Proposition 6.2.5: Algebra with Continuous Functions |
| |
- The identity function f(x) = x is continuous in its domain.
- If f(x) and g(x) are both continuous at x = c,
so is f(x) + g(x) at x = c.
- If f(x) and g(x) are both continuous at x = c,
so is f(x) * g(x) at x = c.
- If f(x) and g(x) are both continuous at x = c,
and g(x) # 0, then f(x) / g(x) is continuous at x = c.
- If f(x) is continuous at x = c, and g(x) is
continuous at x = f(c), then the composition g(f(x)) is
continuous at x = c.
Proof
|
While this proposition seems not very important, it can be used
to quickly prove the following:
| Examples 6.2.6: |
| |
-
 Every polynomial is continuous in R, and every rational function
r(x) = p(x) / q(x) is continuous whenever q(x) # 0.
Every polynomial is continuous in R, and every rational function
r(x) = p(x) / q(x) is continuous whenever q(x) # 0.
-
 The absolute value of any continuous function is continuous.
The absolute value of any continuous function is continuous.
|
Continuity is defined at a single point, and the epsilon and delta
appearing in the definition may be different from one point of
continuity to another one. There is, however, another kind of
continuity that works for all points of domain at the same time.
| Definition 6.2.7: Uniform Continuity |
| |
A function f with domain D is called uniformly
continuous on the domain D if for any
 > 0 there exists a > 0 there exists a
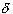 > 0 such that:
if s, t > 0 such that:
if s, t  D and
| s - t | < D and
| s - t | < 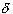 then
| f(s) - f(t) | <
then
| f(s) - f(t) | <  .
Click here for a graphical
explanation. .
Click here for a graphical
explanation.
|

Take a look at this Java applet illustrating uniform continuity.
While this definition looks very similar to the original definition
of continuity, it is in fact not the same: a function can be continuous,
but not uniformly continuous. The difference is that the delta
in the definition of uniform continuity depends only on epsilon,
whereas in the definition of simply continuity delta depends on
epsilon as well as on the particular point c in question.
| Example 6.2.8: |
| |
-
 The function f(x) = 1 / x is continuous on (0, 1). Is it uniformly
continuous there ?
The function f(x) = 1 / x is continuous on (0, 1). Is it uniformly
continuous there ?
-
 The function f(x) = x2 is continuous on [0, 1].
Is it uniformly continuous there ?
The function f(x) = x2 is continuous on [0, 1].
Is it uniformly continuous there ?
-
 The function f(x) = x2 is continuous on
[0,
The function f(x) = x2 is continuous on
[0,  ). Is it uniformly
continuous there ? ). Is it uniformly
continuous there ?
-
 If f(x) is uniformly continuous in R, and
{ xn } is a Cauchy sequence, is the sequence
{ f ( xn ) } also Cauchy ?
If f(x) is uniformly continuous in R, and
{ xn } is a Cauchy sequence, is the sequence
{ f ( xn ) } also Cauchy ?
|
The next theorem illustrates the connection between continuity
and uniform continuity, and gives an easy condition for a continuous
function to be uniformly continuous.
Next, we will look at functions that are not continuous.
 > 0
there exists a
> 0
there exists a
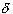 > 0
such that: if
x
> 0
such that: if
x  D
and
| x - c | <
D
and
| x - c | < 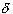 then
| f(x) - f(c) | <
then
| f(x) - f(c) | < 
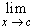 f(x) = f(c).
f(x) = f(c).
 > 0 there exists a
> 0 there exists a
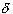 > 0 such that:
if s, t
> 0 such that:
if s, t  D and
| s - t | <
D and
| s - t | < 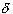 then
| f(s) - f(t) | <
then
| f(s) - f(t) | <  .
Click here for a graphical
explanation.
.
Click here for a graphical
explanation.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  ). Is it uniformly
continuous there ?
). Is it uniformly
continuous there ?