Interactive Real Analysis
- part of Example 7.3.1(b): Oddities of Riemann Integral
Is it true that a function that is constant except at countably many points
is Riemann integrable?
Back
No. Take for example the Dirichlet function, i.e. the function
BackAnother way of declaring that function is to say that g is equal to 0 except for rational values of x, or g is constantly equal to zero except at countably many points. This does not imply that g is continuous except at countably many points - in fact, we have already seen that the function is not continuous anywhere.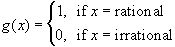
We have already shown that g is not Riemann integrable.
That's odd: Functions that are continuous except at countably many points are Riemann integrable, but there's a function that is constant except at countably many points which is not Riemann integrable.