Examples 7.3.7(e): Measurable Sets
Why these ads ...
Show that the interval
(a,  )
)
is measurable.
Context
We need to show that for every set
A we have that
m*(A)
 m*(A
m*(A  (a,
(a,  ))
+
m*(A
))
+
m*(A  (-
(- , a])
, a])
because
comp(a,  ) = (-
) = (- , a]
, a].
If
m*(A) is infinite, there's nothing to
prove. Therefore we can assume that
m*(A)
is finite. Then, because of the definition of outer measure as an infimum,
there exists a countable collection of open intervals
In
that cover
A and
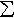 l(In)
l(In)
 m*(A) +
m*(A) + 
for any
 > 0
> 0. Define sets
Jn
and
Kn as
Jn =
In
 (a,
(a,  )
)
Kn =
In
 (-
(- , a])
, a])
Then we have the following properties:
-
Jn
and
Kn
are intervals (or empty) so that
m*(Jn) = l(Jn)
and
m*(Kn) = l(Kn)
and
l(Jn) + l(Kn) =
l(In)
-
Jn
 In
and
Kn
In
and
Kn
 In
so that
In
so that
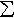 l(Jn)
l(Jn)

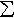 l(In)
and
l(In)
and
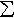 l(Kn)
l(Kn)

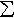 l(In)
l(In)
In particular, all sums are absolutely convergent because the measure of
A is finite.
-
(A
 (a,
(a,  ))
))

 Jn
and
(A
Jn
and
(A
 (-
(- , a])
, a])

 Kn
so that
Kn
so that
m*(A
 (a,
(a,  ))
))
 m*(
m*( Jn)
Jn)

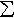 l(Jn)
and
l(Jn)
and
m*(A
 (-
(- , a])
, a])
 m*(
m*( Kn)
Kn)

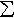 l(Kn)
l(Kn)
because of subadditivity and (1).
But then we have that
m*(A
 (a,
(a,  )) +
m*(A
)) +
m*(A
 (-
(- , a])
, a])

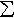 l(Jn) +
l(Jn) +
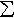 l(Kn) =
l(Kn) =
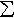 l(Jn) + l(Kn)
=
l(Jn) + l(Kn)
=
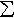 l(In)
l(In)
 m*(A) +
m*(A) + 
Since this inequality holds for every
 > 0
> 0, it implies what
we wanted to prove.
m*(A
(a,
)) + m*(A
(-
, a])
 ) = (-
) = (- , a].
If m*(A) is infinite, there's nothing to
prove. Therefore we can assume that m*(A)
is finite. Then, because of the definition of outer measure as an infimum,
there exists a countable collection of open intervals In
that cover A and
, a].
If m*(A) is infinite, there's nothing to
prove. Therefore we can assume that m*(A)
is finite. Then, because of the definition of outer measure as an infimum,
there exists a countable collection of open intervals In
that cover A and
l(In)
m*(A) +

 > 0. Define sets
Jn
and
Kn as
> 0. Define sets
Jn
and
Kn as
(a,
)
(-
, a])
In and Kn
In so that
In particular, all sums are absolutely convergent because the measure of A is finite.l(Jn)

l(In) and
l(Kn)

l(In)
(a,
))

Jn and (A
(-
, a])

Kn so that
m*(Abecause of subadditivity and (1).(a,
))
m*(
Jn)

l(Jn) and
(-
, a])
m*(
Kn)

l(Kn)
(a,
)) + m*(A
(-
, a])

l(Jn) +
l(Kn) =
l(Jn) + l(Kn) =
l(In)
m*(A) +

 > 0, it implies what
we wanted to prove.
> 0, it implies what
we wanted to prove.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of