Examples 7.3.7(d): Measurable Sets
Suppose A and B are measurable. Then comp(A) and comp(B) are also measurable, and because of the previous exercise the set comp(A)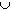 comp(B)
is measurable.
comp(B)
is measurable.
But since
comp(A)the set comp(Acomp(B) = comp(A
B)
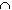 B)
is measurable. Finally, the complement of that set must be measurable,
which is what we wanted to prove.
B)
is measurable. Finally, the complement of that set must be measurable,
which is what we wanted to prove.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of