Examples 7.3.15(a): Monotone sequences of measurable sets
For decreasing sets we had to assume that m(A1)
was finite. Show that without this assumption the statement in the previous
proposition is false.
We have to find a decreasing sequence of sets An such
that lim m(An) is not equal to
m(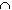 An).
An).
Let An = [n, 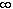 ).
Then m(An) =
).
Then m(An) = 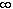 for
all n, so in particular
lim m(An) =
for
all n, so in particular
lim m(An) = 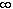 .
.
On the other hand we have that
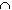 An = 0
so that
m(
An = 0
so that
m( 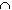 An ) = 0.
That finishes the example.
An ) = 0.
That finishes the example.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of