Examples 7.3.7(b): Measurable Sets

Show that every set with outer measure 0 is Lebesgue measurable.
Context

We need to prove that

m^*(A) = m^*(A E) + m^*(A comp(E))

or because of the subadditivity of outer measure

m^*(A) m^*(A E) + m^*(A comp(E))

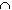But A E 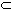E so that we know m^*(A 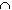E) = 0. On the other hand, A 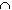comp(E)) 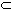A so that m^*(A 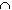comp(E)) m^*(A). But that right away implies that

m^*(A) m^*(A comp(E)) = m^*(A comp(E)) + m^*(A E)

which finishes the proof.

Interactive Real Analysis, ver. 1.9.5
(c) 1994-2007, Bert G. Wachsmuth
Page last modified: Mar 26, 2007