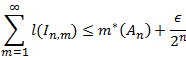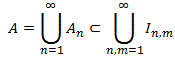Proposition 7.3.4: Properties of Outer Measure
- Outer measure m* is a non-negative set function whose domain is P(R), i.e. the power set of R.
- The outer measure of an interval is its length.
- Outer measure is subadditive, i.e.
m*(A
 B)
B)
 m*(A) + m*(B)
m*(A) + m*(B)
- Outer measure is countably subadditive, i.e. if
{ An } is a countable collection of sets,
then
m*(
 An)
An)

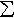 m*(An)
m*(An)
Proof
The first statement is obvious. Outer measure is clearly defined for every set, therefore its domain is P(R). It is also non-negative because all terms involved in the inf are non-negative.
We have already shown that the outer measure of open and closed intervals is their length, so we do not have to prove the second statement again.
The third statement is a warmup exercise for the last statement. Because of the definition of outer measure as infimum, we can find open covers {Ai} of A and {Bi} of B, respectively, such that
l(Ai)
m*(A) +
/2 and
l(Bi)
m*(B) +
/2
But the combined collection
{Ai, Bi}
covers A  B
so that
B
so that
m*(AB)

l(Ai) +
l(Bi)
m*(A) +
/2 + m*(B) +
/2 = m*(A) + m*(B) +

Since this is true for all  it proves
the third statement.
it proves
the third statement.
The proof of the fourth statement, which compared to the previous one might look intimidating because it uses "double indices", is really not that bad: it just switches from adding two terms to adding countably many terms by way of the geometric series. First note that if any of the m*(An) was infinite, the inequality would obviously be true. Thus, we may assume that
m*(An) <for all n
Next, because of the definition of outer measure as an infimum, we know that
for any set An, where n is some fixed
index, there is a sequence of countably many open intervals
In,m such that
An 
 In,m, where
the union is over all m with n fixed, and also, for
any
In,m, where
the union is over all m with n fixed, and also, for
any  > 0:
> 0:
for our fixed n. But now we see that the collection of all (countably many) In,m, ordered somehow, covers A:
so that, using the infimum property again:
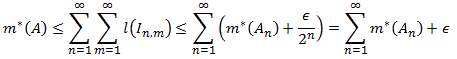
Since this inequality is valid for every  > 0,
it proves subadditivity.
> 0,
it proves subadditivity.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of