Theorem 7.3.8: Properties of Lebesgue measure

  1. All intervals are measurable and the measure of an interval is its length
  2. All open and closed sets are measurable
  3. The union and intersection of a finite or countable number of measurable sets is again measurable
  4. If A is measurable and A is the union of countable number of measurable sets An, then m(A) 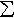m(An)
  5. If A is measurable and A is the union of countable number of disjoint measurable sets An, then m(A) = 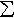m(An)
Context Context

Proof:

First let's review a few facts we have shown before:
  1. The outer measure of an interval is its length
  2. Intervals of the form (a, ) are measurable
  3. Complements of measurable sets are measurable
  4. Union and intersection of two measurable sets are measurable
Also, we need two lemmas that will be useful to show statements 3 and 5.

Lemma 1: Suppose O is a collection of sets such that the union of two elements and the complement of every element from O is again part of O (such a collection is called an Algebra of Sets). If { En } is any countable collection of elements from O then there is another countable collection { Fn } of disjoint elements from O such that En = Fn.

Lemma 2: If E1, E2, ..., En are finitely many disjoint measurable sets, then
m(A (E1 ... En)) = m(A E1) + ... + m(A En)

We will first prove the proposition and give the proofs of these lemmas at the end.

Proof of statement 3: We have already shown that the union and intersection of two measurable sets is again measurable, so we need to prove the statement for countable unions and intersections. Because of facts (3) and (4) measurable sets form an algebra of sets so that it is sufficient to show statement 3 for countable unions of disjoint measurable sets.

Let { En } be a countable collection of disjoint measurable sets and E be their union. Define

Fn = E1 E2 ... En
Because of lemma 2 we have that
m*(A Fn) = m(A E1) + ... + m(A En)
Because comp(E) comp(Fn) we know
m*(comp(E)) m*(comp(Fn))
Thus, for any set A we have:
m(A E1) + ... + m(A En) + m*(A comp(E)) =
      = m*(A Fn) + m*(A comp(E))
      m*(A Fn) + m*(A comp(Fn)) =
      = m*(A)
because the set Fn is measurable. But this is true for any integer n so that
m*(A) m(A En) + m*(A comp(E))
      m(A E) + m*(A comp(E))
because of subadditivity. But that proves that the countable union E of the En is measurable. That countable intersections of measurable sets are measurable follows from de Morgan laws and because complements of measurable sets are measurable.

Proof of statement 1: Let's focus on an open interval (a, b). We know that (a, ) and (-, b] = comp(b, )) are both measurable. But

(-, b) = (-, b-1/n]
Since each set on the right is measurable and countable unions of measurable sets are measurable, intervals of the form (-, b) are also measurable. But
(a, b) = (a, ) (-, b)
so that (a, b) is measurable. Similarly, [a, b] is measurable. Since the outer measure of an interval is its length, and intervals are now measurable, their (Lebesgue) measure must also be their length.

Proof of statement 2: We have shown before that an open set U R can be written as a countable union of open intervals. By (1) intervals are measurable and by (3) countable unions of measurable sets are measurable. Therefore open sets are measurable. But closed sets are the complements of open sets, and complements of measurable sets are measurable. Therefore closed sets are measurable.

Proof of statement 4: This follows immediately from the subadditivity property of outer measure so there is nothing to prove.

Proof of statement 5: In lemma 2 we can set A = R to get that if E1, E2, ..., En are finitely many disjoint measurable sets, then

m(E1 ... En) = m(E1) + ... + m(En)
We now need to make the step to countably many sets. If { Ej } is a countable collection of disjoint measurable sets, then
so that
But for finitely many sets we know that
so that for all n
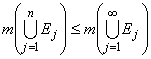
Because that statement holds for all n we conclude that
The reverse inequality follows immediately from subadditivity (statement 4), so that we have proved equality, and hence statement 5.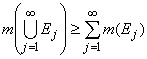

It remains to prove the lemmas we have used.

Proof of Lemma 1: Because A B = comp( comp(A) comp(B)) we know that intersections of two sets from O must also be part of O. The same is true (by induction) for finite unions, intersections, or complements of sets in O.

Now let { En } be a countable collection of sets in O and recursively define sets Fn as follows:

F1 = E1
Fn = En - (E1 ... En-1
for n > 1. Because A - B = A comp(B) all Fn are part of O. It is left as an exercise to show that (i) the Fn are disjoint and (ii) the union of the Fn is the same as the union of the En.

Proof of Lemma 2: First let's show that for two disjoint measurable sets E and F we have

m(A (E F)) = m(A E) + m(A F)
We know that F is measurable, hence
m*(A (E F)) = m*(A (E F) F) + m*(A (E F) comp(F))
But E and F are disjoint so that
A (E F) F = A F
A (E F) comp(F) = A E
Therefore
m*(A (E F)) = m*(A F) + m*(A E)
It is now easy (and left as an exercise) to use induction to finish the proof.

Interactive Real Analysis, ver. 1.9.5
(c) 1994-2007, Bert G. Wachsmuth
Page last modified: Mar 26, 2007