8.4. Taylor Series
In the previous section we discussed the idea of "infinite polynomials": we added terms of the form an (x-c)n and discussed when the resulting infinite function series converges.
We also found that in some cases a power series represents a function that can be expressed in much simpler terms. We found, for example, that:
1 + x + x2 + x3 + ... = 1 / 1-x
for -1 < x < 1 (geometric series function). In fact, if we knew that a power series represents a function f(x) we would also know that the function is infinitely often differentiable and we can differentiate term by term quite easily. For example, take:
f(x) =an(x-c)n = a0 + a1(x-c) + a2(x-c)2 + a3(x-c)3 + ... + an(x-c)n + ...
We can now differentiate n-times and substitute x = c to get:
n f(n)(x) f(n)(c) n=0 f(x) = a0 + a1 (x-c) + a2 (x-c)2 + ... f(c) = a0 n=1 f '(x) = a1 + 2 a2 (x-c) + 3 a3 (x-c)2 + ... f '(c) = a1 n=2 f ''(x) = 2 a2 + 3*2 a3 (x-c) + 4*3 a4 (x-c)2... f ''(c) = 2 a2 n=3 f (3)(x) = 3*2 a3 + 4*3*2 a4(x-c) + 5*4*3 a5(x-c)2 + ... f (3)(c) = 3*2 a3 ... n f (n)(x) = n*(n-1)* ... *1 an + (n+1)*n* ... *2 an+1(x-c) + ... f (n)(c) = n! an
This means that if - for some reason - we know that a function f has a power series representation, then we can easily relate the derivatives of f at c with the coefficients of the power series.
| Proposition 8.4.1: Derivatives of Power Series Function | |
Suppose
f(x) = 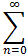 an(x-c)n
is a convergent power series with radius of convergence r > 0.
Then
an(x-c)n
is a convergent power series with radius of convergence r > 0.
Then
an = | |
At first this proposition might seem really useful. It allows us to find the coefficients of a power series by taking derivatives of a given function f. Indeed, that would be useful, but it's not quite what the proposition implies. After all, the assumption is that we already need to know that f has a power series expression. If we do know that, then we can relate the coefficients and the derivatives as indicated. And, of course, it would be interesting only if there was a simpler representation of the function f (such as for our geometric series).
However, that could still be useful in situations such as the examples below. But even better: it will turn out that for many functions f we can use the above relation to find the coefficients after all, even if we don't know a priory the power series for f. That's going to be a "big deal" theorem we'll introduce in a little while. For know, let's work with what we have:
| Example 8.4.2: Derivatives of Power Series | |
| |
If a power series does represent an underlying function then it gets a special name.
| Definition 8.4.3: Taylor Series | |
Suppose f is an infinitely often differentiable function on a
set D and c  D.
Then the series D.
Then the series
Tf(x, c) =is called the (formal) Taylor series of f centered at, or around, c. If c = 0 the series is sometimes also called MacLaurin Series, i.e. a MacLaurin series is a Taylor series around zero. | |
It is important to note the following:
- A Taylor series is associated with a given function f. A power series, on the other hand, contains (in principle) arbitrary coefficients an. Thus, every Taylor series is a power series but not every power series is a Taylor series.
- A Taylor series converges trivially for x = c, but it may or may not converge anywhere else. In other words, the radius of convergence of a Taylor series is not necessarily greater than zero
- Even if a Taylor series converges, it may or may not converge to the original function f
Let's start with a few simple examples of well-known Taylor series.
| Example 8.4.4: Taylor Series | |
|
| |
Here is an interesting example that shows that even if a function f is infinitely often differentiable, the resulting Taylor series does not necessarily converge to the original function.
| Example 8.4.5: A Taylor Series that does not Converge to its Function | |
| |
Now that we know how bad the situation can get, we need a theorem that lets us determine when a Taylor series does converge to the original function. Note that since a Taylor series is a power series we already know how to find the radius of convergence, but we don't (yet) know what the series converges to. The next theorem will solve that problem:
| Theorem 8.4.6: Taylor's Theorem | |
Suppose f  Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c  [a,b] we have: [a,b] we have:
f(x) =where Rn+1(x) = 1/n!In particular, the Taylor series for an infinitely often differentiable function f converges to f if and only if the remainder R(n+1)(x) converges to zero as n goes to infinity. | |
This theorem has important consequences:
- A function that is (n+1)-times continuously differentiable can be approximated by a polynomial of degree n
- If f is a function that is (n+1)-times continuously differentiable and f(n+1)(x) = 0 for all x then f is necessarily a polynomial of degree n.
- If a function f has a Taylor series centered at c then the series converges in the largest interval (c-r, c+r) where f is differentiable.
Taylor's Theorem involves a remainder, and one way to show that a function really has a Taylor seriess is to prove that the remainder goes to zero. It helps to have different versions of the remainder, thus:
| Proposition 8.4.8: Lagrange Version of Taylor Remainder | |
Suppose f  Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c  [a,b] we have: [a,b] we have:
f(x) =where R(n+1)(x) =for some t between x and c. | |
This form of the remainder is useful to prove a corollay, which we state, with a suitable application, as an example.
| Example 8.4.9: Applying the Lagrange Remainder | |
 [a, b],
then [a, b],
then
f(x) =where r(x) goes to zero as x goes to c. | |
The remainder, in one form or another, can now be used to prove that some functions can be expressed as a Taylor series.
Well-Known Taylor Series
You must, without fail, memorize the following Taylor series. They can be used to easily prove facts that are otherwise difficult, or had to be taken on trust until know.
| Proposition 8.4.10: The Geometric Series | |
1/1-x = 1 + x + x2 + x3 + x4 + ... = | |
| Proposition 8.4.11: Taylor Series for the Exponential Function | |
ex = 1 + x + 1/2! x2 + 1/3! x3 + 1/4! x4 + ... = | |
Fun Facts:
- eix = cos(x) + i sin(x) (Euler's Formula)
- (cos(x) + i sin(x))n = cos(nx) + i sin(nx) (De Moivre's Formula)
ex = ex and
ex = ex
| Proposition 8.4.12: Taylor Series for the Cosine Function | |
cos(x) = 1 - 1/2! x2 + 1/4! x4 - 1/6! x6 + ... = | |
Fun Facts:
- cos(0) = 1
- cos is an even function, i.e. cos(-x) = cos(x)
- cos(x -
/2) = -sin(x)
cos(x) = - sin(x)
| Proposition 8.4.13: Taylor Series for the Sine Function | |
sin(x) = x - 1/3! x3 + 1/5! x5 - 1/7! x7 + ... = | |
Fun Facts:
- sin(0) = 0
- sin is an odd function, i.e. sin(-x) = -sin(x)
- sin(x -
/2) = -cos(x)
sin(x) = cos(x)
The series for ex, sin(x), and cos(x) converge for all x. For series with a finite radius of converges we mentioned before that you need to consider the boundaries of the interval of convergence separately. For example, the geometric series converges for |x| < 1 and diverges for x = -1 as well as for x = 1. What about a series that converges to a function inside |x - c| < r, but the series also converges at one (or both) endpoints. Does it then necessarily converge to the same function? To answer that question we need one more theorem:
| Theorem 8.4.14: Abel's Limit Theorem | |
If a power series
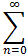 an xn
has radius of convergence r, and an xn
has radius of convergence r, and
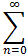 an rn
also converges, then an rn
also converges, then
| |
As prime examples we introduce the series expansion for ln and arctan
| Proposition 8.4.15: Taylor Series for the Natural Log | |
ln(1+x) = x - 1/2 x2 + 1/3 x3 - 1/4 x4 + .... = | |
Fun Facts:
- ln(2) = 1 - 1/2 + 1/3 - 1/4 + ... (but convergence is slow)
| Proposition 8.4.16: Taylor Series for the Arc Tan | |
arctan(x) = x - 1/3 x3 + 1/5 x5 - 1/7 x7 + ... = | |
Note that the series converges at both endpoints.
Fun Facts:
/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
Functions that can be expressed as a Taylor series are the "nicest" functions that analysis has to offer. Not only are the infinitely 'smooth' but they can also be differentiated and integrated easily (in their series representation), and approximated to arbitrary accuracy by polynomials. They deserve a special name:
| Definition 8.4.17: Real Analytic Functions | |
| A function f that can be expressed as a power series with non-empty radius of convergence is called a real analytic function. | |
The name is borrowed from Complex Analysis, where we talk about analytic functions. But while there are many possibilities to check whether a complex function is analytic, it is generally tricky to decide if a function is real analytic. But as a non-mathematical rule of thumb: if a function is infinitely often differentiable and is defined in one line, chances are that the function is real analytic.
To actually find the series, a variety of techniques are available.
Techniques to find Taylor series:
We will conclude our discussion by describing a few standard tricks to find Taylor series.
Use Taylor's formula: Apply Taylor's formula an =
to find the an (usually not your first choice).
- Find MacLaurin series for f(x) =
and guess what the general binomial series for (1+x)a might be.
Substitution: Start with a known series and perform some substitution
- Find MacLaurin series for f(x) = 1/1 + x2
Differentiation: Start with a known series and differentiate both sides
- Find a series for f(x) = 2x/(1-x2)2
Integration: Start with a known series and integrate both sides
- Which function is represented by the series
1/n xn
Multiplication: Multiply two known series together until a pattern emerges:
- Find the Taylor series centered at zero for f(x) = x2 e2x. Find the first 3 terms of the Taylor series centered at zero for g(x) = sin(2x) ex2
Division: Use division to divide two known series until a pattern emerges:
- Find the Taylor series centered at zero for f(x) = sin(x)/x. Find the first 3 non-zero terms of the Taylor series centered at zero for g(x) = tan(x)
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 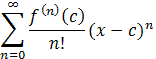
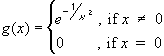 . Show that:
. Show that:
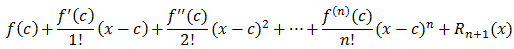
 (x-t)nf (n+1)(t) dt
(x-t)nf (n+1)(t) dt
 ex2 dx
ex2 dx
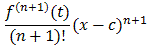
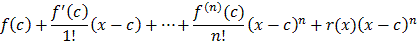
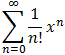 for all x
for all x
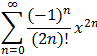 for all x
for all x
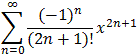 for all x
for all x
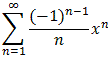 for -1 < x
for -1 < x  1
1
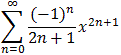 for |x|
for |x|