Proposition 8.4.13: Taylor Series for the Sine Function
The proof is analogous to the proof for the cos-function. Please look up that proof and adjust it to this situation.
Fun Facts:
- sin(0) = 0
- sin is an odd function, i.e. sin(-x) = -sin(x)
- sin(x -
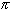 /2) = -cos(x)
/2) = -cos(x) 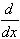 sin(x) = cos(x)
sin(x) = cos(x)
The fun facts are all easy and are left as exercises. For the third fact you
might start with f(x)=cos(x) and develop that in a series around
c = 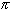 /2.
/2.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 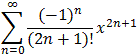 for all x
for all x