Interactive Real Analysis - part of MathCS.org

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 8.1. Pointwise Convergence
• 8.2. Uniform Convergence
• 8.3. Series and Power Series
• 8.4. Taylor Series
• 8.5. Approximation Theory
• 9. Historical Tidbits
• Java Tools

Example 8.4.7 (b): Using Taylor's Theorem

Why these ads ...

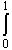The function f(x) = e^x2 does not have a simple antiderivative. Use Taylor's theorem to find an approximate value for e^x2 dx

Back

Taylor's theorem basically says: if a nicely differentiable function is too complicated, you may replace it, approximatel, by a suitable polynomial. In this case it is not possible to find an antiderivative for our function so will go the "Taylor route" to find an approximate answer. As usual, we need to compute various derivatives, but first we need to settle on a center for our series. Two different choices seem reasonable:

• choose c=0 because derivatives at 0 should be easy to compute
• choose c=1/2 because we want to integrate between 0 and 1 so selecting a value in the middle should provide a better approximation

We also need to settle on a degree for our polynomial: the higher the degree the better the approximation, but the more derivatives we might have to find. Let's - for no particular reason - settle on a second-degree polynomial. Here are the various values at the two different centers:

	c = 0	c = 1/2
f(x) = ex2	f(0) = 1	f(1/2) = e1/4 = 1.284
f '(x) = 2x ex2	f '(0) = 0	f '(1/2) = e1/4 = 1.284
f ''(x) = (2 + 4x2) ex2	f ''(0) = 2	f ''(1/2) =3 e1/4 = 3.852

Thus, we get two different second-degree polynomials:

• Center c=0: p(x) = 1 + 2/2 x²
• Center c=1/2: p(x) = 1.284 + 1.284 (x-0.5) + 3.852/2 (x-0.5)²

Here are the graphs of these two polynomials in comparison with the original function for 0 < x < 1:

1 + 2/2 x2	1.284 + 1.284 (x-0.5) + 3.852/2 (x-0.5)2

When we finally approximate our integral, we get:

• Center c=0: 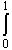e^x2 dx 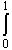1 + 2/2 x² dx 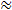4/3 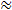1.3333
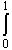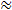
• Center c=0.5: e^x2 dx 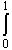1.284 + 1.284 (x-0.5) + 3.852/2 (x-0.5)² dx 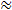1.4445

A more sophisticated computer program computes 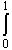e^x2 dx 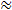1.462651746. Thus, our polynomial centered at c=1/2 gives a significantly better approximation.