MathCS.org - Real Analysis: Example 8.4.5: A Taylor Series that does not Converge to its Function

Example 8.4.5: A Taylor Series that does not Converge to its Function

Define 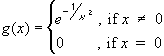. S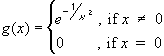how that:

The function is infinitely often differentiable

The Taylor series T_g(x, 0) around c = 0 has radius of convergence infinity.

The Taylor series T_g(x, 0) around c = 0 does not converge to the original function.

Back

We have already shown before that:

g is infinitely often differentiable
g⁽ⁿ⁾(0) = 0 for all n

The Taylor series of g is therefore:

T_g(x, 0) = a_n xⁿ = 1/n! g⁽ⁿ⁾(0) xⁿ = 0 xⁿ = 0 for all x

In particular, the radius of convergence is infinity. But the original function is not identically equal to zero (g(0) = 0 but g(x) > 0 for x # 0), so that:

T_g(x, 0) # g(x) unless x = 0

Next | Previous | Glossary | Map | Discussion

Interactive Real Analysis - part of MathCS.org

Example 8.4.5: A Taylor Series that does not Converge to its Function