Proposition 8.4.11: Taylor Series for the Exponential Function
We know - assuming the assumptions of Taylor's theorem are satisfied (which they are) - that:
|f(x) -| = |Rn+1(x)|
where I can pick my preferred form of the remainder. Let's pick the regular remainder with c = 0:
|Rn+1(x)| = 1/n! |(x-t)nf (n+1)(t) dt | = 1/n! |
(x-t)n et dt |
e|x|/n! |
(x-t)n dt |
e|x|/(n+1)! |x|n+1
But for a fixed x we have already shown before that for any fixed number x
|x|n/n! = 0
which finishes the proof.
Fun Facts:
- eix = cos(x) + i sin(x) (Euler's Formula)
- (cos(x) + i sin(x))n = cos(nx) + i sin(nx) (De Moivre's Formula)
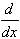 ex = ex and
ex = ex and
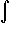 ex = ex
ex = ex
- i2 = -1
- i3 = i2 i = -1 i = -i
- i4 = i2 i2 = (-1) (-1) = 1
- i5 = i4 i = i
- i6 = i4 i2 = -1
- ...
If we now substitute ix into the series expression for the exponential function we get:
eix = 1 + (ix) + 1/2! (ix)2 + 1/3! (ix)3 + 1/4! (ix)4 + 1/5! (ix)5 + 1/6! (ix)6 + 1/7! (ix)7 + ...
= 1 + ix - 1/2! x2 - i 1/3! x3 + 1/4! x4 + i 1/5! x5 - 1/6! x6 - i 1/7! x7 + ...
= 1 - 1/2! x2 + 1/4! x4 - 1/6! x6 + ... + ix - i 1/3! x3 + i 1/5! x5 - i 1/7! x7 + ...
=+ i
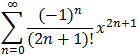
= cos(x) + i sin(x))
assuming we know the series expansions for sin and cos.
Fact 2: De Moivre's Formula (cos(x) + i sin(x))n = cos(nx) + i sin(nx) is now merely an application of the Euler's Formula together with the properties of the exponential functions:
(cos(x) + i sin(x))n) = (eix)n = einx = ei (nx) = cos(nx) + i sin(nx)
Fact 3: We may have proved that elsewhere, so this would be a good review exercise.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 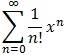 for all x
for all x