Proposition 8.4.15: Taylor Series for the Natural Log
ln(1+x) = x - 1/2 x2 + 1/3 x3 - 1/4 x4 + .... =Note that the series also converges for x = 1.for -1 < x
1
Instead of applying Taylor's theorem directly, we'll start with the geometric series and integrate both sides:
1/1+x dx =
1/1-(-x) dx =
=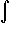
(-x)n dx =
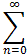
(-x)n dx =
=(-1)n/n+1 xn+1 =
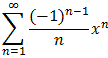
where the computation is valid for -1 < x < 1. It remains to prove the statement for x = 1. But this will be a perfect application of Abel's Limit theorem:
converges for |x| < 1
converges as the alternating harmonic series
Therefore
ln(2) =ln(1+x) =
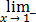
=
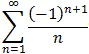
according to Abel's Limit theorem.
Fun Facts:
- ln(2) = 1 - 1/2 + 1/3 - 1/4 + ... (but convergence is slow)
This fact has just been proven as an application of Abel's Limit theorem.
Alt. Harmonic Series approaching ln(2)=0.6931472
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of