MathCS.org - Real Analysis: Example 8.4.2 (b): Derivatives of Power Series

Example 8.4.2 (b): Derivatives of Power Series

Assume again that f(x) = e^2x has a convergent power series expression, but this time centered at c = 1. Find the coefficients of this power series.

Back

This time we assume our function can be represented as

e^2x = a_n(x-1)ⁿ = = a₀ + a₁(x-1) + a₂(x-1)² + a₃(x-1)³ + ...

Then, as before

a_n =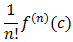

Again we need to find the n-th derivative of the function f at the center of the series. Taking derivatives on both sides and substituting 1 (the center in this example) we get:

n=0 f(x)=e^2x f(1)=e

n=1 f '(x)=2 e^2x f '(1)=2 e²

n=2 f ''(x)=2²e^2x f ''(1)=2² e²

n=3 f ⁽³⁾(x)=2³e^2x f ⁽³⁾(1)=2³ e²

Therefore, if e^2x had a series representation centered at c = 1 it would be:

e^2x = ^2ⁿ/_n! e² (x-1)ⁿ

Next | Previous | Glossary | Map | Discussion

n=0	f(x)=e^2x	f(1)=e
n=1	f '(x)=2 e^2x	f '(1)=2 e²
n=2	f ''(x)=2²e^2x	f ''(1)=2² e²
n=3	f ⁽³⁾(x)=2³e^2x	f ⁽³⁾(1)=2³ e²

Interactive Real Analysis - part of MathCS.org

Example 8.4.2 (b): Derivatives of Power Series