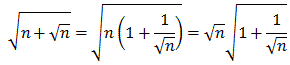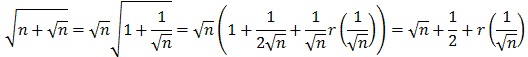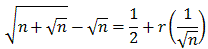Example 8.4.9: Applying the Lagrange Remainder
Show that if f is n-times continuously differentiable
on [a, b] and c  [a, b],
then
[a, b],
then
 [a, b],
then
[a, b],
then
f(x) =where r(x) goes to zero as x goes to c.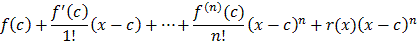
Use this result and the function
f(x)=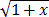 to show that
to show that
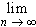
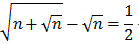
The first statement is a straight-forward application of the Lagrange remainder theorem - try it youself!
As for the application, let
f(x)=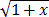 , which is continuously
differentiable around c = 0. According to our statement (and taking
the first derivative at zero) we have:
, which is continuously
differentiable around c = 0. According to our statement (and taking
the first derivative at zero) we have:
= 1 + x/2 + x r(x)
for some r(x) with
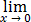 r(x) = 0. To
apply this to our problem, we need to see
r(x) = 0. To
apply this to our problem, we need to see 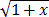 involved somehow. Therefore we factor an n to get:
involved somehow. Therefore we factor an n to get:
Now we can apply our approximation to the second root, with
x = 1/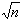 , to get:
, to get:
Therefore
which, together with the fact that
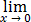 r(x) = 0
will do the trick.
r(x) = 0
will do the trick.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of