Example 8.4.18 (d): Finding Taylor Series by Integration
Start with a known series and integrate both sides.
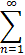 1/n xn
1/n xn
Example
Which function is represented by the series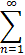 1/n xn
1/n xn
Our known series with which to start is, once again, the Geometric series. For variety, let's use t as variable:
1/1-t =tn =
tn-1
Integrating both sides gives:
1/1-t dt =
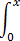
tn-1 dt =
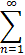
tn-1 dt =
1/n xn
Thus, the function represented by this series is:
1/n xn =
1/1-t dt = -ln(1-x)
1/n xn
f(x) = -ln(1-x)
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of