Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 7.1.6(a):

Suppose f(x) = x2-1 for x in the interval [-1, 1]. Find:
  1. The left and right sums where the interval [-1, 1] is subdivided into 10 equally spaced subintervals.
  2. The upper and lower sums where the interval [-1, 1] is subdivided into 10 equally spaced subintervals.
  3. The upper and lower sums where the interval [-1,1] is subdivided into n equally spaced subintervals.
For the first two questions we can again use a Java applet that will perform the computations for us. Here is are the results computing the left and right sums.

Note, in particular, that right and left Riemann sums are the same (an accident ?). The upper and lower sums are similarly computed, noting that in the interval [0, 1] the largest value of x2-1 over any subinterval inside [0, 1] is always the right endpoint, while the smallest value occurs on the left endpoint. For subintervals inside [-1, 0] it is just the other way around.

Note that this time the values don't agree but we have that L(f, P) U(f, p), which is again no accident.

To answer the last question we can not use the above Java applet because we don't know a numeric value for n. Here is the appropriate manual computation for the, say, the upper sum: We are looking for n equally spaced subintervals of [-1, 1] so that our partition consists of the points:

xj = -1 + j * 2/n
where j = 0, 1, ..., n and | P | = 2/n.

Case 1: n is even, i.e. n = 2 N for some integer N

The renumbered partition now is:

xj = -1 + j * 1/N
where j = 0, 1, ..., N, N+1, ..., 2 N. In that case the point 0 is part of the partition (take j = N). The point to notice before we can begin the computation is that the function is decreasing over the interval [-1, 0] and increasing over the interval [0, 1]. That implies that for all partition points less than 0 the maximum of f occurs on the left endpoint, for points bigger than 0 the maximum occurs on the right. Hence:
U(f, P) =
In appropriate "sigma" notation we therefore have: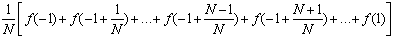
U(f, P) =
      =
      =
      =
      =
      =
      =
      =
We have used the results on the sum of square integers mentioned in the chapter on Induction to simplify the various sums.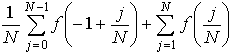

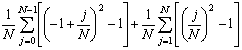
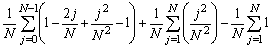
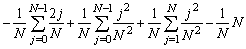
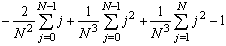
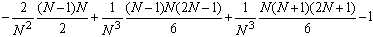
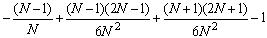
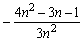
We can verify our formula by looking at the above applet. There the 10-upper sum computes to -1.119999. In our formula we need to let N = 5 because 10 = n = 2 N. Substituting N = 5 gives the exact value of -1.12 for the 10-th upper sum.

The case where n is odd, as well as the computation of the lower sum, is left as an exercise. There's nothing new in those computations (but for n odd there's something special happening at 0), it's just somewhat tedious. You can check whichever formulas you come up with against the numeric answers of the above applet.

Next | Previous | Glossary | Map | Discussion