Interactive Real Analysis
- part of Example 2.3.12: Sum of Squares and Cubes
- The sum of the first n numbers is equal
to
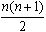
- The sum of the first n square numbers is
equal to
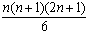
- The sum of the first n cubic numbers is
equal to
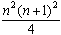
BackActually, as the story goes, the young Gauss, who later became a famous mathematician, was once in grade school. His teacher, who did not want to teach anything, asked his students to compute the sum of the first 100 integers, thinking that this would give him plenty of time to read a newspaper. However, after a few seconds the young Gauss came up with the correct answer, much to the dismay of his teacher.
How was Gauss able to find the answer so quickly ? He certainly did not know about induction, so he used the following trick. We want to find 1 + 2 + 3 + ... + n-1 + n. Instead of finding that sum once, we compute it twice, calling the unknown answer S. We list the numbers once in forward and once in backward order:
Each column except the last adds up to n+1, and there are n of them. The last column adds up to 2 S, so that we have the equation:
1 + 2 + 3 + ... + (n-1) + n = S n + (n-1) + (n-2) + ... + 2 + 1 = S
n (n+1) = 2 Sfrom which the result follows.
2. Let's prove the second statement via induction.
Property Q(n):
1 + 22 + 32 + ... + n2 =Check Q(1):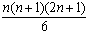
1 = 1 × 2 × 3 / 6 = 1which is true. Now assume Q(n) is true, let's prove Q(n+1):
1 + 22 + 32 + ... + n2 + (n+1)2 =The last expression is exactly property Q(n+1), which finishes the induction proof.
=
==
==
=
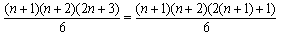
3. We will - of course - leave the third statement as an exercise. It may be that the last step requires some factorization that may or may not be easy to do. Instead, try working your way 'backward'. For example, instead of trying to factor an expression such as 2 n2 + 7n + 6, you could start with the answer you are hoping to get, in this case (n + 2)(2n + 3), and work your way back.