2.5. Pi and e are irrational
Pi and e (Euler's number) are two numbers that occur everywhere in mathematics. Both are irrational and in fact transcendental numbers. In this little appendix we will prove that both numbers are irrational. We will not show that they are also transcendental numbers. The proofs will actually use tools from much later sections, but they might be interesting nevertheless, and the results fit well in this section.First will now prove that e (Euler's number) is irrational. In fact, it is a transcendental number, but that requires a lot of work to prove.
| Theorem 2.5.3: e is irrational | |
| Euler's number e is irrational | |
Proof: We know that for any integer n
(check the definition of Euler's number and the definition of Euler' series) where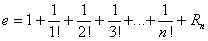
Now suppose that e was rational, i.e. there are two positive integers a and b with e = a / b.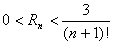
Choose n > b. Then, using the above representation, we have:
or multiplying both sides by n! we get: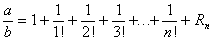
Since n > b, the left side of this equation represents an integer, and hence n! Rn is also an integer. But we know that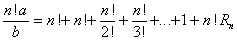
so that if n is large enough the left side is less than 1. But then n! Rn must be a positive integer less than 1, which is a contradiction.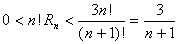

Next we prove that Pi is irrational, which is a lot harder to do. We need a preliminary result:
| Lemma 2.5.1: | |
Define a function fn(x) = 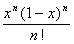 . Then this function
has the following properties: . Then this function
has the following properties:
| |
Proof: Using the binomial theorem, we see that when the numerator of the function is multiplied out, the lowest power of x will be n, and the highest power is 2n. Therefore, the function can be written as
fn(x) =where all coefficients are integers. It is clear from this expression that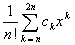
.gif) = 0 for
k < n and for k > 2n.
= 0 for
k < n and for k > 2n.
Also, looking at the sum more carefully, we see that
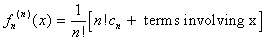
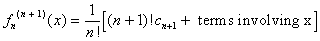
...
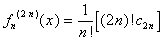
But this implies that .gif) is an integer for any k.
is an integer for any k.
Moreover, since
we also have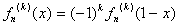
Therefore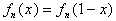
.gif) is an integer
for any k.
is an integer
for any k.
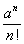 | <
| <  for n large enough ( n > 2a) and any
a. Now we can prove the result of this chapter:
for n large enough ( n > 2a) and any
a. Now we can prove the result of this chapter:
| Theorem 2.5.2: Pi is irrational | |
| Pi is irrational | |
Proof: We will prove that 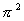 is not rational, which implies the assertion. Suppose it was rational. Then
there are two positive integers a and b with
is not rational, which implies the assertion. Suppose it was rational. Then
there are two positive integers a and b with
Define the function= a / b
Each of the factors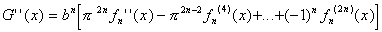
is an integer, by assumption on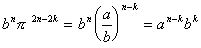
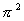 .
We also know that
.
We also know that
.gif) and
and
.gif) are integers as well.
Hence, G(0) and G(1) are both integers.
are integers as well.
Hence, G(0) and G(1) are both integers.
Differentiating G(x) twice, we get:
The last term in this equation, the (2n+2)-th derivative, is zero, by the properties of the function f. Adding G(x) and G''(x) we get: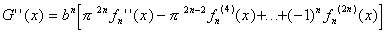
Now define another function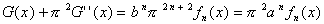
Then, using the above formula for G(x) +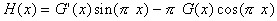
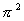 G''(x), we have:
G''(x), we have:
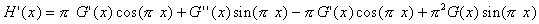
=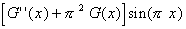
=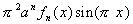
Now we can use the second fundamental theorem of calculus to conclude:
Thus, the integral= H(1) - H(0)
=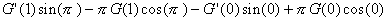
=[ G(1) + G(0)]
is an integer. But we also know that 0 < fn(x) < 1 / n! for 0 < x < 1. Therefore, estimating the above integral, we get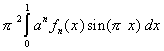
0 <for 0 < x < 1. Therefore, we can estimate our integral to get<
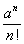
0 <Here we have used the fact that the last fraction approaches zero if n is large enough. But now we have a contradiction, because that integral was supposed to be an integer. Since there is no positive integer less than 1, our assumption that<
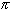
< 1
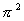 was rational resulted in a
contradiction. Hence,
was rational resulted in a
contradiction. Hence, 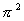 must
be irrational.
must
be irrational.

This prove is, admittedly, rather curious. Aside from the assumption that Pi is rational (leading to the contradiction) the only other properties of Pi that are really involved in this proof are that
sin(and we need the defining properties of the trig. functions that) = 0, cos(
) = 1
sin'(x) = cos(x), cos'(x) = - sin(x), sin(0) = 0, cos(0) = 1That does not make the proof much clearer, but it illustrates that some essential properties of
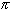 are indeed used along the
way, and this proof will not work for any other number.
are indeed used along the
way, and this proof will not work for any other number.
Publish or Perish, Inc, 1980, pages 307 - 310
Contributed to this page: Thomas Wollmann
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of