Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 7.1.17(b):

Let
where p, q relatively prime and q > 0, and assume g is restricted to [0, 1]. Is g Riemann integrable ? If so, what is the value of the integral ?
We have seen this function before, where we have shown that it is continuous at all irrational numbers and discontinuous at the rationals. In particular, the function has countably many points of discontinuity. Since the discontinuities are dense, i.e. they are "all over" the interval [0, 1] it might seem that it is difficult to find the value of the integral (if the function is Riemann integrable). But with the theoretical background we developed so far it will be easy to compute the answer.

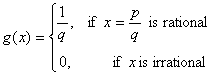
Having countably many discontinuities, we know by our previous theorem that the function is Riemann integrable and it remains to find the value of the integral.

Take any partition P = {x0, x1, ..., xn} and look at:

dj = inf{g(x): x [xj-1, xj]}
Since every subinterval [xj-1, xj] contains irrational numbers we clearly have that dj = 0 for all j. But then the lower integral I*(g) = sup{ L(g,P): P a partition of [a, b]} must also be 0.

Since g was integrable the upper and lower integral agree so that

g(x) dx = 0
for a = 0 and b = 1.
Next | Previous | Glossary | Map | Discussion