Countable Discontinuities

The function g is continuous precisely at the irrational numbers, and discontinuous at all rational numbers.
Back

Incidentally, it is impossible to have a function that is continuous only at the rationals, which will be proved in the section on Metric spaces and Baire categories.

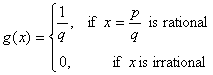
Proof:

The actual proof is left as an exercise. However, you may want to make use of the following fact:

Lemma
If r = p / q is a rational number (in lowest terms) define a function with domain Q via f(r) = 1 / q. Then the limit of f(r) as r approaches any real number is zero.

Proof of Lemma:

Take any sequence { r_n } of rational numbers converging to a fixed number a (which could be rational or irrational). Since the sequence converges, it is bounded. For simplicity assume that all rational numbers r_n are in the interval [0, K] for some integer K. Now take any > 0 and pick an integer M such that 1 / M < . Because each rational number is the quotient of two positive integers, we have:

at most K of the rational numbers r_n in the interval [0, N] can have denominator equal to 1
at most 2 K of the rational numbers r_n in the interval [0, N] can have denominator equal to 2
...
at most M * K of the rational numbers r_n in the interval [0, N] can have denominator equal to M

In total, at most finitely many of the r_n can have a denominator less than or equal to K. That means, however, that there exists an integer N such the denominator of r_n is bigger than M for all n > N. But then

| f(r_n) | < 1 / M < for all n > N

Since > 0 was arbitrary, that means that the limit of f(r_n) must be zero, as needed. Our assumption that the numbers r_n were all positive can easily be dropped, and a similar proof would work again.

Using this lemma it should not be too hard to prove the original assertion.

Interactive Real Analysis, ver. 1.9.5
(c) 1994-2007, Bert G. Wachsmuth
Page last modified: Mar 26, 2007