Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 7.1.4:

Suppose f(x) = x2 on [0, 2]. Find
  1. the fifth Riemann sum for an equally spaced partition, taking always the left endpoint of each subinterval
  2. the fifth Riemann sum for an equally spaced partition, taking always the right endpoint of each subinterval
  3. the n-th Riemann sum for an equally spaced partition, taking always the right endpoint of each subinterval.
The right and left Riemann sums are illustrated in the Java applet below. To verify the result of that applet, let's perform the computation manually as well.

The interval is [0, 2], and we want to find the fifth Riemann sum. Therefore the partition we need is:

x0 = 0, x1 = 2/5 = 0.4, x2 = 4/5 = 0.8,
x3 = 6/5 = 1.2, x4 = 8/5 = 1.6, x5 = 10/5 = 2
with a norm of | P | = 0.4. Taking the right points of each of the resulting intervals we can compute the right Riemann sum as:
f(0.4)×0.4 + f(0.8)×0.4 + f(1.2)×0.4 + f(1.6)×0.4 + f(2)×0.4 =
      = 0.4×(f(0.4) + f(0.8) + f(1.2) + f(1.6) + f(2)) =
      = 0.4×(0.42 + 0.82 + 1.22 + 1.62 + 22) =
      = 0.4×(0.16 + 0.64 + 1.44 + 2.56 + 4) =
      = 0.4×8.8 = 3.52
The left Riemann sum, correspondingly, computes to:
f(0.0)×0.4 + f(0.4)×0.4 + f(0.8)×0.4 + f(1.2)×0.4 + f(1.8)×0.4 =
      = 0.4×(f(0.0) + f(0.4) + f(0.8) + f(1.2) + f(1.6)) =
      = 0.4×(02 + 0.42 + 0.82 + 1.22 + 1.62) =
      = 0.4×(0 + 0.16 + 0.64 + 1.44 + 2.56) =
      = 0.4×4.8 = 1.92
For the last part we can not use our Java applet since we do not have a numerical value for n. But we can manually compute the answer as follows: subdividing [0, 2] into n equal subintervals gives the partition:
xj = j×2/n, where j=0, 1, ... n
Taking the right endpoint of all resulting subintervals and substituting them into the Riemann sum formula gives:
R(f, P) = f(2/n) × 2/n + f(4/n) × 2/n + ... + f( (n-1) 2/n ) + f(n 2/n)
which works out to
R(f, P) = 2/n × ( (1 × 2/n)2 + (2 × 2/n)2 + ... + ( (n-1) × 2/n )2 + (n × 2/n)2)
We can factor out 4/n2 to get:
R(f, P) = 8/n3 × (12 + 22 + ... + (n-1)2 + n2)
In the chapter on induction we have shown that the sum of the first n square numbers equals 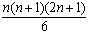so that we now have:
R(f, P) = 8/n3 × = 4/3 × (n+1) × (2n+1) / n2
We can substitute n = 5 to verify our formula:
R(f, Pn=5 ) = 4/3 ×6 ×11 / 25 = 88/25 = 3.52
just as computed above.
Next | Previous | Glossary | Map | Discussion