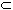 Z
Z
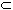 Q
Q
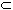 R
R
1.1. Complex Numbers | ICA |
Natural numbers (N), integers (Z), rational numbers (Q), and real numbers (R) should be quite familiar by now. Each more advanced set includes the previous one, and indeed extends its properties:
NZ
Q
R
- N derives from simple counting numbers, but addition does not have an inverse
- Z adds inverse numbers with respect to addition, but multiplication does not have an inverse
- Q adds inverse numbers with respect to multiplication, but the limit process is not complete
Example 1.1.1: Properties of number systems Find
- a natural number without an additive inverse
- an integer without a multiplicative inverse
- a sequence of rational numbers that converges but the limit is not rational
R, the set of real numbers, on the other hand, is (by definition) complete with respect to the limiting and has all properties that are useful in daily life. We can add, subtract, multiply, and divide (albeit not by zero), we can take limits of real numbers and get back other real numbers, and any two real numbers are comparable (i.e. either they are identical or one is smaller than the other). Such a system, incidentally, is called a field:
Definition 1.1.2: A Field A field is a set F together with two operations commonly denoted as + and *, as well as two different special elements commonly denoted as 0 and 1, that satisfies the following axioms:
- Both + and * are associative, i.e. a+(b+c)=(a+b)+c and a*(b*c)=(a*b)*c
- Both + and * are commutative, i.e. a+b=b+a and a*b=b*a
- The distributive law holds, i.e. a*(b+c)=(a*b)+(a*c)
- 0 is the additive identity, and 1 is the multiplicative identity, i.e. for all x we have x+0=x and x*1=x
- There are additive and multiplicative inverses, i.e. for all x exists y such that x+y=0 and for all non-zero a exists b such that a*b=1
In other words, R is a field where in addition the limit process works (the proper way of saying it is that R is a complete field). The above properties just formalize in general some of the properties of real numbers, addition, and multiplication that we use (seemingly) automatically.
Example 1.1.3: Is Q a field Is Q a field?
So, what is wrong with R to - possibly - warrant yet another number system? One problem is that:
not every polynomial equation is solvable in R
In other words:
We can certainly live with those facts, but they seem not logical (as Mr. Spock from the USS Enterprise would say): the third eqution should really have three solutions, not just 1, and the fourth equation should have two, not zero, solutions! The solution to the problem will come from a simple, yet ingenious definition:
Definition 1.1.4: The Imaginary Unit Define a new symbol called the imaginary unit, or i, as: i =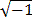
This may not make sense, since traditionally we are not allowed to take
even roots of negative numbers. However, this is a definition so
henceforth the symbol i simply means: square root of negative
one. If you are worried, think about another, probably more familiar
symbol: 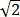 . It looks familar, but
what does it really mean? Of course it simply means that it is that symbol
that by definition solves the equation x2-2=0, just as
i or
. It looks familar, but
what does it really mean? Of course it simply means that it is that symbol
that by definition solves the equation x2-2=0, just as
i or 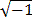 will be that symbols
that solves x2+1=0.
will be that symbols
that solves x2+1=0.
What matters are the consequences and reprecussions that the introduction, or definition, of a new symbol has: does it result in any contradictions to known results? Does it yield new results that are compatible - but perhaps extend - existing theorems? Is it 'useful'?
Just as the symbol 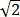 provides a reason of
extending the rational numbers to the real ones, the symbol
i =
provides a reason of
extending the rational numbers to the real ones, the symbol
i = 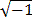 will cause us to extend
the real numbers to the complex numbers (a step that we will formally
do below).
will cause us to extend
the real numbers to the complex numbers (a step that we will formally
do below).
Example 1.1.5: Properties ofi Use the definition of i to:
Using our new symbol we could define a new number system: informally we simply combine real numbers with our new symbol as:
z = x + i*y, where x, yR
We can use the definition of i to add, subtract, multiply, and divide such entities. For example:
The new number system could now consist of all symbols of the
form x + i*y, but we will use a more formalized approach to avoid
the somewhat strange symbol i (just in case someone still
objects to it). Just as 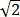 is not used in the
definition of the real numbers, the symbol i should not be used
in the formal definition of the complex numbers.
is not used in the
definition of the real numbers, the symbol i should not be used
in the formal definition of the complex numbers.
Definition 1.1.6: Complex Numbers The set of complex numbers C is defined as the set of all pairs (x,y) , x, y R, where for z = (x,y) and w = (u, v) we define:
Two complex numbers z1 = (x1,y1) and z2 = (x2,y2) are called equal if both x1 = x2 and y1 = y2. We will frequently use the symbol 0 to mean (0,0).
- z + w = (x,y) + (u,v) = (x+u, y+v)
- z * w = (x,y) * (u,v) = (x*u - y*v, x*v + y*u)
This definition does not pull any strange symbols out of the hat (i
is nowhere to be seen), but it does look perhaps a little contrived: addition of
two tuples is defined as it should, but why is multiplication defined so strangely?
![]() Why not simply define (x,y) * (u,v) = (x u, y v)?
Why not simply define (x,y) * (u,v) = (x u, y v)?
Please note that two complex numbers being equal results in two equations that need to be true simultaneously. You should also observe that we have defined equality of two complex numbers, but not inequality. In other words, we can not decide if one complex number is less or greater than another! But first we want to find out what this definition has to do with our new symbol i. Let's play with the definition to find out:
Example 1.1.7: Simple Complex Numbers
Now we can formalize the properties of our new set of numbers:
Theorem 1.1.8: Complex Numbers are a Field The set of complex numbers C with addition and multiplication as defined above is a field with additive and multiplicative identities (0,0) and (1,0). It extends the real numbers R via the isomorphism (x,0) = x. We define the complex number i = (0,1). With that definition we can write every complex number interchangebly as
z = (x,y) = x + i*y = x + i y
Complex numbers are an extension of the reals, but not all properties of real numbers extend to complex ones: the real numbers are ordered, i.e. two real numbers are either equal or one is great than the other. Complex numbers, however, are not ordered: two complex numbers are either equal or not, but if they are not equal we can not decide which one is greater.
We now have two representations of the field of complex numbers:
- as pairs of real numbers (x,y) with a 'funny' multiplication
- as a sum of two real numbers z = x + iy using the symbol i with the property that i2 = -1
The first definition is the mathematically proper one, since it does not need a new symbol. However, the second definition is the easier one to work with in almost all situations, and we will hence think of complex numbers as:
Complex Numbers
C = {z = x+iy, where x,yR and i2 = -1}
Let's put our new numbers to work:
Example 1.1.9: Algebra with complex numbers
Now we can also remedy, at least partially, our original problem where polynomial equations of degree 2 sometimes have two, one, or no solution.
Now we have an elementary understanding of complex numbers, but to better work with them we need a helpful visual representation. That will be the topic of the next section.
Proposition 1.1.10: Two complex roots Show that every equation z2 = c has exactly two solutions in C (unless c = 0). In other words, every complex (non-zero) number c has exactly two complex square roots.