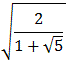Solve the equations
- z2 = i and
- z2 = 1+2i
Example 1.1.9 (d): Algebra with complex numbers |
Solve the equations |
We represent z = x + iy and expand the first equation:
z2 = (x + iy)2 = x2 - y2 + i 2xy = i
Now we equate like terms (real and imaginary parts of the equation) to arrive at a system of two equations with two unknowns:
(1) x2 - y2 = 0
(2) 2xy = 1
The first equation implies that x = y or x = -y.
Using this in the second equation gives
x = 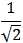 or
x = -
or
x = -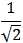 .
Thus, the two roots of i are:
.
Thus, the two roots of i are:
z1 =+ i
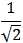
z2 = -- i
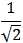
We proceed similar for the second equation:
z2 = (x + iy)2 = x2 - y2 + i 2xy = 1 + 2i
Again we equate like terms to arrive at a system of two equations with two unknowns:
(1) x2 - y2 = 1
(2) 2xy = 2
Our system of equations is a little harder than before, but it's not too bad. Solving the second equation for y (we can exclude x=0 as a possible solution) gives y = 1/x. We can substitute that into the first equation to get:
x2 - 1/x2 = 1
We multiply through with x2 and bring everything on one side:
x4 - 1 - x2 = 0
You should have no trouble solving this equation, using the quadratic formula and a substitution like u = x2. You should give some thought as to why there will be two answers, because you might think at first there should be four. Here are the two answers so you can double-check your work:
z1 =+ i
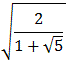
z2 = -- i