If we did define this "silly" multiplication, the resulting system would no longer be a field! Recall the last axiom for a field. It says, in part:

There is a multiplicative inverse, i.e. for all non-zero a exists b such that a*b=1

This axiom implies the cancellation property:

if ac = bc and c is not zero then a = b

But if we define (x,y)*(u,v) = (xu, yv) we have, with c = (0,1) 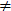(0,0):

(1,0)*c = (0,0)*c yet (1,0) (0,0)

Phrased more succinctly: if we defined multiplication via the above "silly" multiplication, and we insisted on the field axioms, then we could prove that any number is zero! That's indeed silly!