Find
- a natural number without an additive inverse
- an integer without a multiplicative inverse
- a sequence of rational numbers that converges but the limit is not rational
Example 1.1.1: Properties of number systems |
Find |
1. In N no number except zero has an additive inverse. For example, there is no natural number you can add to 2 to get zero.
2. In Z no number except for 1 has a
multiplicative inverse. For example, there is no integer you can multiply with
2 to get 1.
3. In Q every number has additive and multiplicative inverses, but let's consider the sequence {xn} where
x1 = 2
xn = 1/2 (xn + 2/xn) for n > 1
Each of the xn is clearly a rational number, but it can be shown that
xn =
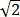
But the square root of 2 is not rational and hence is not in Q.